Aplicações de Derivadas
Reta Tangente
Do gráfico 1, deduziu-se que 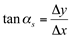 , além disso,
, além disso, 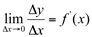 que é a definição de derivada de uma função. Sabe-se da geometria analítica, que o coeficiente angular “m” de uma reta é a tangente trigonométrica da inclinação desta reta. Entende-se como inclinação o menor ângulo positivo que a reta faz com o eixo
que é a definição de derivada de uma função. Sabe-se da geometria analítica, que o coeficiente angular “m” de uma reta é a tangente trigonométrica da inclinação desta reta. Entende-se como inclinação o menor ângulo positivo que a reta faz com o eixo 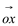 . Portanto, conclui-se que
. Portanto, conclui-se que 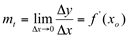 isto é, o coeficiente angular da reta tangente a uma curva em um ponto específico é a derivada desta função na abscissa deste ponto. Esta é a interpretação geométrica de derivada.
isto é, o coeficiente angular da reta tangente a uma curva em um ponto específico é a derivada desta função na abscissa deste ponto. Esta é a interpretação geométrica de derivada.
Ex5. Determine as equações das retas tangente e normal à curva 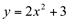 no ponto
no ponto 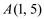 .
.
Resolução:
Primeiro, vamos determinar a primeira derivada da função dada: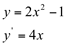
Para encontrarmos o coeficiente angular da reta tangente a essa curva, substituímos a abscissa do ponto A na função derivada: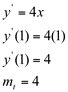
A seguir, escrevemos a equação da reta tangente, usando a fórmula da geometria analítica para a equação de uma reta que passa por um ponto conhecido e tem coeficiente angular m.

Uma reta normal a uma curva, em um ponto, é uma reta perpendicular à reta tangente, nesse mesmo ponto. Como retas perpendiculares têm coeficientes angulares inversos e simétricos, fica fácil a determinação da equação da reta normal:

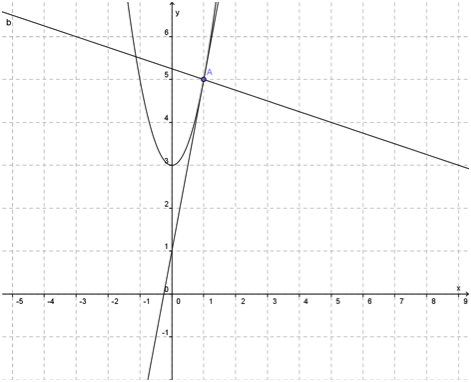
O gráfico abaixo, ilustra esta situação:
Taxa de Variação
Velocidade e Aceleração
Sabe-se da Física, que a velocidade escalar média é a razão entre o a variação do espaço percorrido pela variação do tempo:
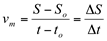
Veja que é uma função razão incremental. Levando-se ao limite quando o acréscimo dado a variável independente tende a zero, temos a função derivada do espaço percorrido em relação ao tempo. Esta derivada é denominada de velocidade instantânea, em um instante de tempo determinado:
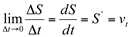
Da mesma forma, define-se aceleração escalar média como a razão entre a variação da velocidade pela variação do tempo:
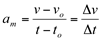
Esta aceleração também é uma razão incremental. Calculando-se o limite desta razão,quando o acréscimo dado a variável independente tende a zero, obtém-se a função derivada da velocidade em relação ao tempo decorrido. Tem-se, então, a velocidade instantânea em um determinado tempo específico.
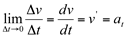
Em termos práticos, dada uma função do espaço percorrido em função do tempo, a primeira derivada dessa função, em relação ao tempo é a equação da velocidade e, a segunda derivada, em relação ao tempo, é a equação da aceleração.
Ex6. A posição de um corpo, em um instante t é dada por 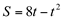 Considerando t expresso em segundos e S em metros, determine:
Considerando t expresso em segundos e S em metros, determine:
- A equação da velocidade;
- A equação da aceleração;
- A velocidade quando
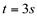
- A aceleração no instante
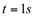
Solução:
a)

b)

c)
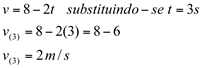
d)
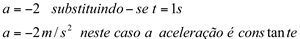
Máximos e Míninos e Estudo do Crescimento de uma Função
Para iniciarmos este estudo, vamos primeiro relacionar o sinal derivada de uma função com os intervalos onde a mesma é crescente, decrescente ou constante.
Observe os gráficos abaixo:
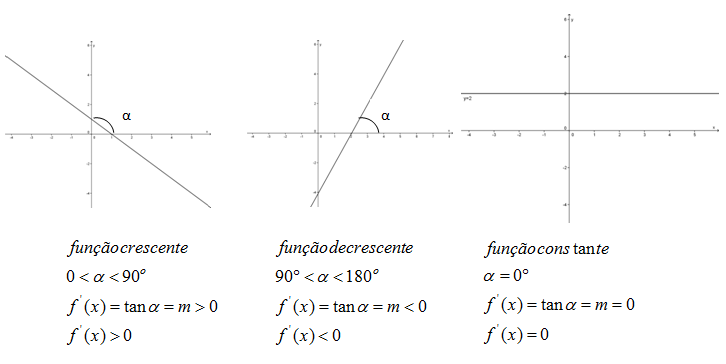
Resumindo, temos:
- Uma função é crescente em um determinado intervalo, se e somente se sua derivada, neste intervalo, é positiva.
- Uma função é decrescente em um determinado intervalo, se e somente se, sua derivada, neste intervalo, é negativa.
- Uma função é constante em um determinado intervalo, se e somente se, sua derivada é igual a zero.
Observe o gráfico abaixo da função 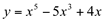
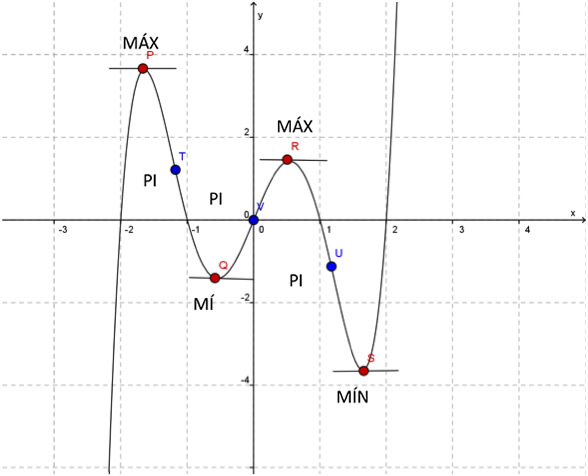
Veja que nos pontos P, Q, R e S a derivada se anula, pois as tangentes a esses pontos são paralelas ao eixo dos xx. Em linguagem matemática podemos escrever 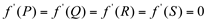 .
.
Em torno do ponto P a função passa de crescente para decrescente, ou seja, a sua derivada muda o seu sinal de positiva para negativa. Neste caso, este ponto P, em que 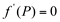 é denominado de Ponto de Máximo Local.
é denominado de Ponto de Máximo Local.
Já no entorno do ponto Q, a função muda de decrescente para crescente, então o sinal de sua derivada passa de negativo para positivo. Assim, este ponto Q, onde 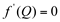 é chamado de Ponto de Mínimo Local.
é chamado de Ponto de Mínimo Local.
Da mesma forma, o ponto R é outro ponto de máximo local dessa função, enquanto que o ponto S é outro ponto de mínimo local.
Uma função pode apresentar vários pontos de máximo e de mínimo. Ter um ponto de máximo, não significa necessariamente que este seja o maior valor dessa função, ao passo que ter um ponto de mínimo, também não significa necessariamente o menor valor que a função assume. Há também funções que não apresentam nem pontos de máximo nem de mínimo.
Para se determinar intervalos de crescimento e decrescimento e pontos de máximo e de mínimo de uma função, é preciso verificar os pontos onde a derivada dessa função se anula ou pontos para os quais esta derivada não está definida. Feito isto, analisa-se o sinal da derivada em torno desses pontos.
Ex7. Da função 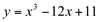 determine se houver:
determine se houver:
- intervalos de crescimento e decrescimento;
- pontos de máximo e de mínino;
Solução:

Estas raízes, por anularem a primeira derivada, são candidatas a serem as abscissas de pontos de máximo ou de mínimo. Para isso, vamos analisar o sinal da função derivada, 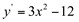 , em torno dessas raízes:
, em torno dessas raízes:
Uma das formas de se fazer essa análise, é a de calcular valores numéricos da função derivada, para pelo menos um valore menor que a menor raiz, para um valor entre as raízes e um valor maior que a maior raiz.
Neste caso, tem-se:
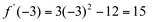 (significa que a função derivada assume valores positivos à esquerda de -2).
(significa que a função derivada assume valores positivos à esquerda de -2).
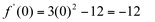 (significa que a função derivada assume valores negativos entre -2 e +2).
(significa que a função derivada assume valores negativos entre -2 e +2).
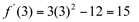 (significa que a função derivada assume valores positivos à direita de +2).
(significa que a função derivada assume valores positivos à direita de +2).
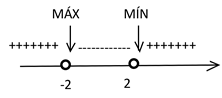
Lembrando que uma função é crescente no intervalo em que sua derivada é positiva e decrescente no intervalo em que sua derivada é negativa, conclui-se então:
Função Crescente: C: 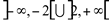
Função Decrescente: D: 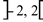
Com esta análise, conclui-se que em há um ponto de máximo, pois a derivada se anula e muda o seu sinal de positivo para negativo. Em há um ponto de mínimo, porque a derivada se anula e troca o seu sinal de negativo para positivo.
Para determinarmos as ordenadas desses pontos, fazemos o cálculo dos valores numéricos da função, nas abscissas indicadas:
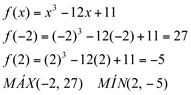
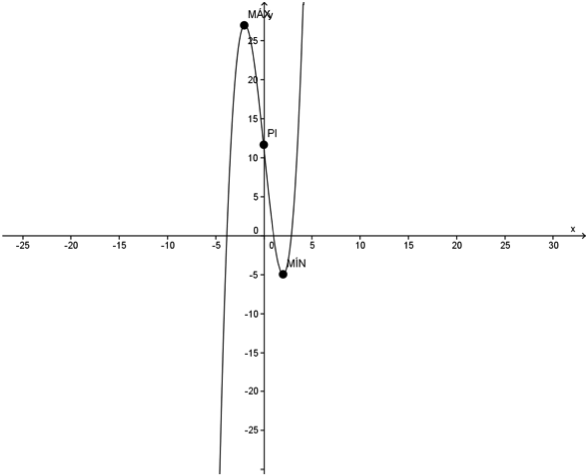
Para verificação desses resultados, observe o gráfico da função
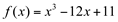 abaixo:
abaixo:
Ex8. Para a função 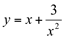 determine, se houver:
determine, se houver:
- intervalos de crescimento e decrescimento;
- pontos de máximo e de mínimo;
Solução:

Esta função, bem como a sua derivada, não estão definidas no ponto 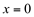 . Este ponto, portanto, será considerado na análise do sinal da derivada:
. Este ponto, portanto, será considerado na análise do sinal da derivada:
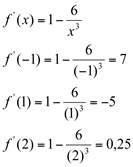
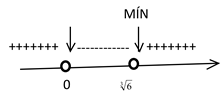
Neste caso, mesmo a derivada tendo mudado o seu sinal de positiva para negativa, em torno do ponto 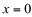 , não é um ponto de máximo, pois não é possível calcular
, não é um ponto de máximo, pois não é possível calcular 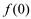 .
.
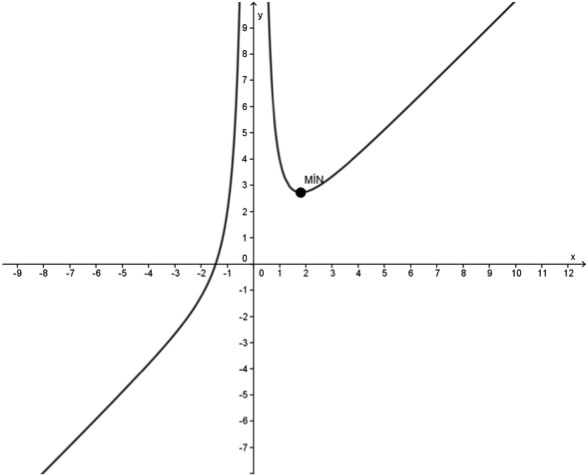
Esta função é:
Crescente: C: 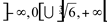
Decrescente: D: 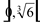
Determinação do ponto de mínimo:
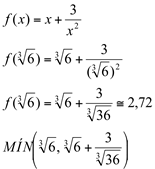
Confirmamos estas informações observando o gráfico de 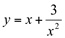 :
:
Pontos de Inflexão e Estudo do Sentido da Concavidade de uma Função
Observe no gráfico da função 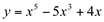 os pontos T, V e U. Verifica-se que estes pontos separam arcos de concavidades contrárias. O ponto T separa um arco de concavidade para baixo de um arco com concavidade para cima. Já o ponto V separa um arco de concavidade para cima de outro de concavidade para baixo. E o ponto U faz a separação de um arco côncavo para baixo de um côncavo para cima. Estes pontos são denominados de Pontos de Inflexão (PI).
os pontos T, V e U. Verifica-se que estes pontos separam arcos de concavidades contrárias. O ponto T separa um arco de concavidade para baixo de um arco com concavidade para cima. Já o ponto V separa um arco de concavidade para cima de outro de concavidade para baixo. E o ponto U faz a separação de um arco côncavo para baixo de um côncavo para cima. Estes pontos são denominados de Pontos de Inflexão (PI).
Definição de Concavidade
Se uma função f for diferenciável em um intervalo aberto I, então o gráfico de f é:
- côncavo para cima em I, se f’ é crescente em I;
- côncavo para baixo em I, se f’ é decrescente em I.
Teste de Concavidade
Se a derivada segunda f’’ existe em um intervalo aberto I, então o gráfico de f é:
- côncavo para cima em I, se f’’(x)>0 em I;
- côncavo para baixo em I, se f’’(x)<0, em I.
Resumindo, uma função apresentará um ponto de inflexão, se este ponto anular a segunda derivada e se em torno desse ponto, a segunda derivada mudar o seu sinal de positivo para negativo ou vice-versa. Se num determinado intervalo, o sinal da segunda derivada for positivo, o gráfico dessa função é côncavo para cima, nesse intervalo, se, ao contrário, o sinal da segunda derivada for negativo, então o gráfico apresenta uma concavidade para baixo, nesse intervalo.
Ex9. Da função 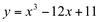 determine, se houver:
determine, se houver:
- intervalos com o sentido da concavidade;
- pontos de inflexão.
Resolução:

Analisando o sinal de f’’:
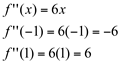
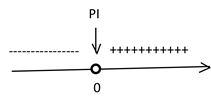
Em torno do ponto 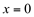 , f’’ altera o seu sinal, portanto, esta função apresenta as seguintes concavidades:
, f’’ altera o seu sinal, portanto, esta função apresenta as seguintes concavidades:
C.P.C. (concavidade para cima): 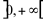
C.P.B. (concavidade para baixo): 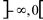
Determinação do ponto de inflexão :
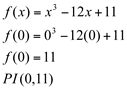
Lembrete: No estudo do sinal da função derivada, seja da primeira ou da segunda, deve-se levar em consideração:
- os pontos que anulam f’ e f’’.
- os pontos onde f’ e f’’ não estejam definidos.
Teorema de Cauchy
Sejam 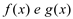 duas funções contínuas em
duas funções contínuas em 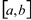 , deriváveis em
, deriváveis em 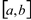 e
e 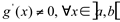 , então existe
, então existe 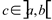 tal que:
tal que:
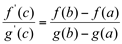
Regra de L'Hospital
Sejam duas funções 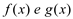 que satisfazem ao teorema de Cauchy e
que satisfazem ao teorema de Cauchy e 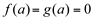 .
.
Se 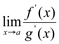 existe então existe
existe então existe 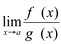 e,
e, 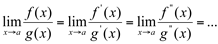
Observação: A regra de L’Hospital é usada para a resolução de limites indeterminados dos tipos 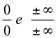 .
.
Ex8. Determine o valor de 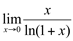 .
.
Solução:
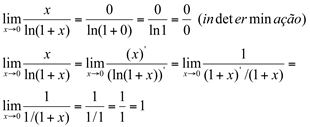
Ex9. Calcule 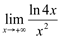
Solução:
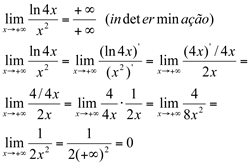
Ex10. Calcular 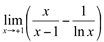
Solução:
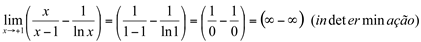
Neste caso, vamos transformar esse limite em um do tipo 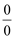 .
.
