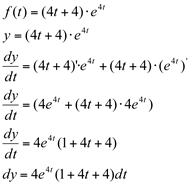Estudaremos nesta unidade um operador denominado Integral. Este operador é aplicado às funções e se constitui de um processo inverso ao da derivação.
Para se chegar ao conceito de integral, é preciso definir-se primeiro o conceito de Diferencial.
Definição de Diferencial de uma Função
No gráfico abaixo, marcam-se os seguintes elementos:
f-> função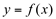 
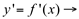função derivada de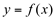 
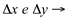acréscimos dados as variáveis x e y, respectivamente
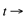reta tangente a função 
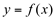no ponto A (xa,ya)
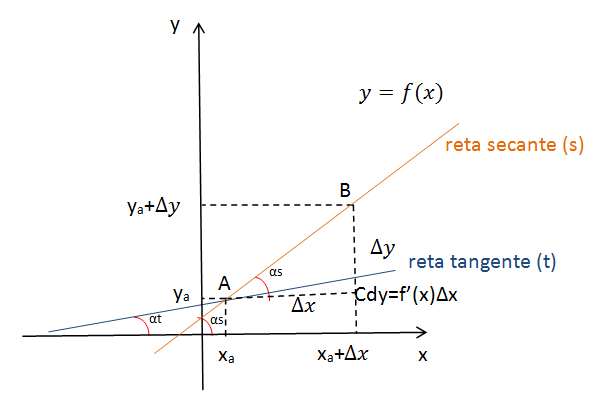
As variações de x e y sobre a reta tangente são as diferenciais dx e dy, respectivamente de um ponto P sobre a curva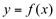 
.
Sabe-se que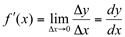 
, ou seja ,Dx = dx e Dy =dy, ou de outra forma f(x0+Dx) = f(x0) + f ‘(x0).Dx.
Então dy e dx estão relacionadas por dy = f ‘(x)dx, onde dy = f ‘(x0)dxé chamado de diferencial de uma função f no ponto x0.
Portanto, dy = f ‘(x)dxé a diferencial da função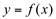 
Ex1. Calcular a diferencial da função f dada por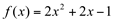 
.
Solução:
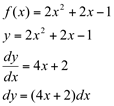
Ex2. Determine a diferencial da função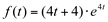 
Solução:
