Definição de Integral de uma Função
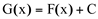, onde 
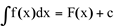e c é uma constante arbitrária denota a família de todas as antiderivadas de f(x) em um intervalo I. Convém observar que essas famílias de antiderivadas diferem entre si apenas por essa constante arbitrária.
Observações:
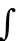->símbolo ou sinal de integral (soma)
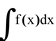->integral indefinida
f(x)dx-> elemento de integração ou integrando.
f(x) ->função integrada.
dx-> diferencial da integração.
x-> variável de integração.
C-> constante de integração.
Para esclarecer melhor essa situação vamos calcular a diferencial das seguintes funções:
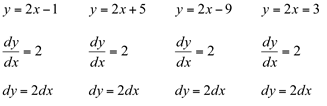
Observa-se que todas estas funções que diferem entre si apenas por uma constante, apresentam a mesma derivada e a mesma diferencial. Dizemos, então, que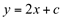 
é uma função primitiva de 
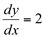e que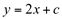 
é uma integral indefinida de 
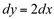. Em simbologia matemática, expressamos:
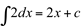
Propriedades:
Sejam f(x) e g(x) duas funções diferenciáveis e que tenham uma antiderivada em algum intervalo I . Então:
1)
(i)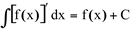 
(ii)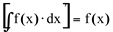 
2)
(i)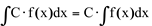 
(ii)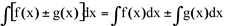 
Observamos que os operadores, derivação e integração não são operadores inversos, mas sim podemos dizer que existe um processo inverso entre esses operadores.