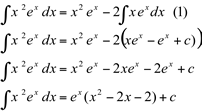Integração Por Partes
Muitas vezes, não é possível integral uma função usando apenas a substituição de variável, pois não se consegue calcular a diferencial exata.
Vejamos: calcule 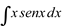
Ao fazermos, 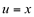 temos que
temos que 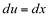 .Deveria ser
.Deveria ser 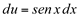 Neste caso, a diferencial que encontramos não é a exta. Nem se fizermos
Neste caso, a diferencial que encontramos não é a exta. Nem se fizermos 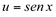 , com
, com 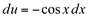 .A diferencial exata, deveria ser
.A diferencial exata, deveria ser 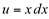
Para esses casos, precisamos usar uma técnica de integração denominada Integração por Partes.
Sejam u = f(x)e v = g(x) duas funções diferenciáveis. Então a diferencial do produto y = u . v = f(x) . g(x)e´ dy = ( u . v’ + v . u’ ) dx
dy = u.v’dx + v.u’dx como 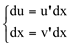 podemos escrever:
podemos escrever:
dy = udv+vdu, como dy = d(uv) temos d(uv) = udv+vdu que é a diferencial do produto de duas funções.
Agora, integrando os demais membros, temos:
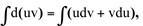 pela propriedade de integral indefinida.
pela propriedade de integral indefinida.
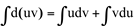
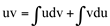 , daí:
, daí:
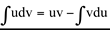 -> Fórmula da integração por partes.
-> Fórmula da integração por partes.
Ex8. Calcular 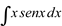
Fazendo, 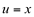 então
então 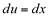
Fazendo, 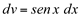 então
então 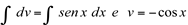
Substituindo em 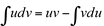 , vem que
, vem que
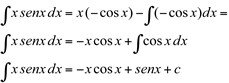
Ex9. Calcular 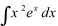
Fazendo, 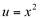 então
então 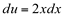
Fazendo, 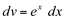 então
então 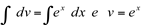
Substituindo em 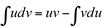 , vem que
, vem que
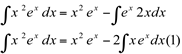
Para calcular 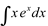 usamos a integração por partes novamente:
usamos a integração por partes novamente:
Fazendo, 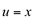 então
então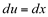
Fazendo, 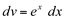 então
então 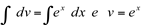
Substituindo em 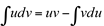 , vem que
, vem que
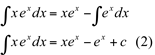
Substituindo (2) em (1), temos: