Integração de Funções que Contém Trinômios do 2° Grau
A resolução de integrais que apresentam trinômios do 2º grau requer que esse trinômios sejam fatorados em uma soma ou diferença de dois quadrados.
Inicialmente, revisamos a obtenção de um quadrado perfeito.
Transformamos o trinômio num quadrado perfeito:
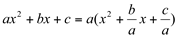
Fazemos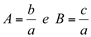 
, temos um trinômio sem o coeficiente de x2: 
.
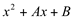O termo B é sempre igual ao quadrado da metade de A.
De um modo geral:
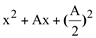, é um quadrado perfeito 
.
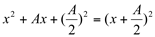Vejamos os exemplos resolvidos a seguir:
Resolver:
Ex10.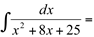 
Resolução:
Primeiro, vamos transformar o trinômio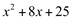 
em uma soma de quadrados:
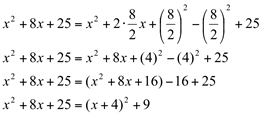
Feito isso, a integral é escrita assim:
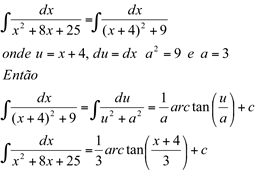
Ex11.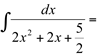 
Fatorando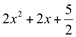 
, temos que
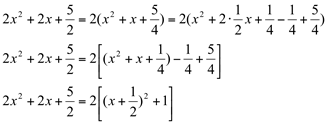
Substituindo na integral, vem:
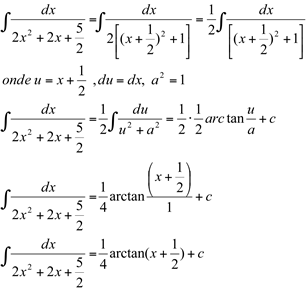
Ex12.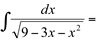 
Fatorando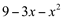 
vem que:
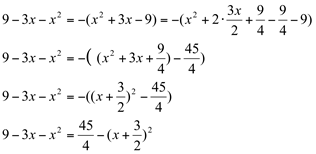
Substituindo na integral, temos:
