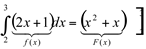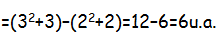Integral Definida
Até agora estudamos as integrais indefinidas, isto é, aquelas que possuem infinitas diferenciais, com todas diferindo-se entre si por apenas uma constante.
No caso de uma integral definida, o resultado não é uma infinidade de funções, mas sim, um número. Estas integrais possuem diversas aplicações, como o cálculo de áreas de figuras planas e de volume de sólidos de revolução, por exemplo.
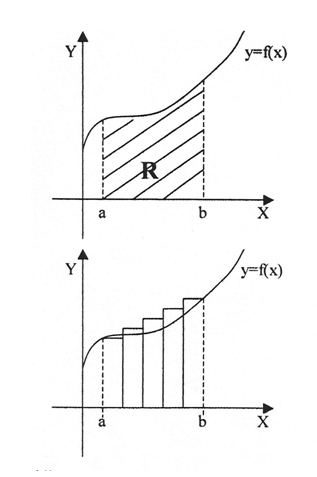
Veja o gráfico abaixo, que representa a área de uma região R compreendida entre uma função e o eixo das abscissas:
Como determinar a área dessa região? Observe que R possui um lado curvo, então as fórmulas da geometria plana servem apenas para obter-se um resultado aproximado.
Podemos formar n retângulos, no intervalo de a até b. Para obter-se a área aproximada, basta calcular a área de cada retângulo e fazer o somatório delas.
Dividimos o intervalo (a,b) em “n” partes:
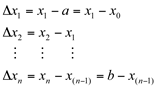Tornando: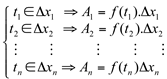 
Podemos formar a seguinte soma, representativa da área de todos os retângulos.
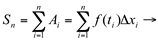Soma de Riemann
Se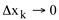 
, a soma Sn se aproxima da área exata limitada pelas curvas, o eixo x e as ordenadas em x=a e x=b isto é:
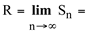
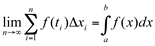
ou seja:
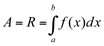que é chamada de INTEGRAL DEFINIDA ou INTEGRAL DE RIEMANN de f(x) entre os limites "a" e "b".
Teorema Fundamental do Cálculo Integral
Se f(x) é continua em [a,b] e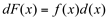 
, então: 
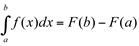, ou então, 
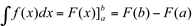, sendo F(x) uma primitiva de f(x).
Ex13:
Calcule a integral definida:
