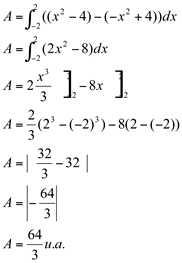Área de Figuras Planas por Integração
Nem sempre uma integral definida corresponde a uma área plana, compreendida entre a função que define a curva e os eixos coordenados. Para tal, é necessário que, no intervalo considerado, a curva esteja totalmente acima ou abaixo com o eixo das abscissas.
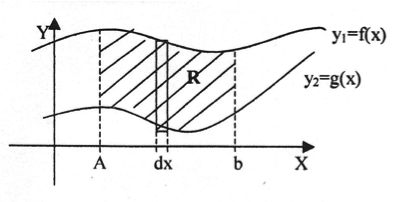
Observe o gráfico abaixo. Dadas as funções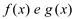 
definidas no intervalo 
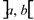, sendo 
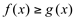para todo o x em 
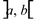. Então a área compreendida entre as curvas é definida por 
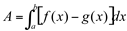onde 
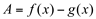representa a altura e dx a base do retângulo.
Exemplos Resolvidos:
Ex14.
Determine a área compreendida entre a curva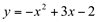 
e acima do eixo ox.
Solução: Determinando os zeros e o vértice da função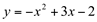 
.
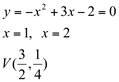
Esboçando o gráfico de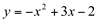 
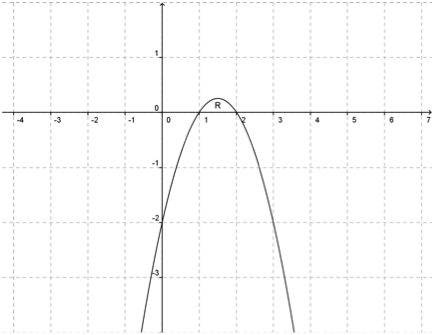
Esta área será igual a seguinte integral:
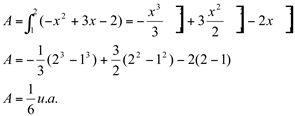
Ex15. Calcular a área delimitada entre as curvas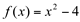 
e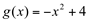 
Solução:
Calculando os zeros de cada função e os pontos de intersecção entre elas:
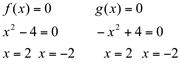
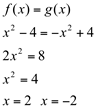
Construindo o esboço do gráfico d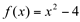e 
e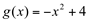 
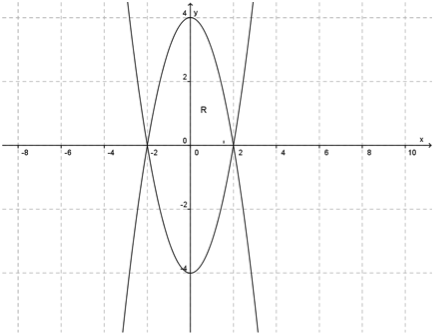
Neste caso a área R compreendida entre as duas funções é calculada por:
