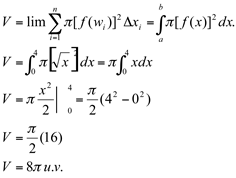Volume dos Sólidos de Revolução
Outra aplicação importante de integrais definidas é o cálculo de volume de sólidos de revolução, ou seja, aqueles que são formados pela rotação completa de 360° de uma figura plana em torno de um eixo, que é chamado de eixo de revolução.
No gráfico abaixo, considera-se um plano perpendicular ao eixo ox passando pela abscissa w, intercepta o sólido, obtendo-se uma secção transversal circular com raio f(w) e área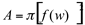 
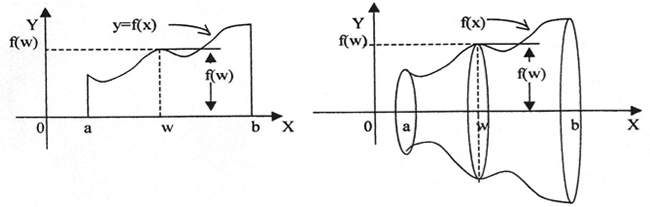
Se considerarmos uma espessura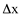 
na seção transversal circular, obteremos 
.
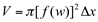Se dividirmos o sólido em “n” partes, obteremos V1,V2,V3,....,Vn, volumes.
Portanto, o volume total aproximado do sólido de revolução será: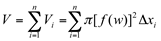 
, que pode ser considerada como uma Soma de Riemann, fazendo n(x)=
.
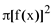Definição
Seja f, contínua em [a,b]. O volume V do sólido de revolução gerado pela rotação da região R determinada pelos gráficos de f,x=a, x=b e do eixo dos OX é dado por:
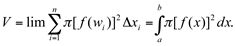
A definição acima pode ser generalizada para outras situações:
- A função f(x) é negativa em alguns pontos de [a,b].
Como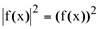 
, a fórmula acima é válida neste caso.
- A região de rotação R está entre os gráficos de duas funções f(x) e g(x) de a até b.
Supondo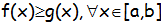 
o volume do sólido de revolução, gerado pela rotação da região R em torno do eixo ox, é dado por
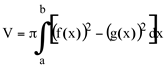
- A rotação se efetua ao redor de uma reta paralela a um dos eixos coordenados.
Se o eixo de revolução for a reta y=C, temos
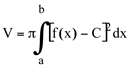
Ex16. Determine o volume da região R delimitada, em IR2 por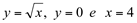 
em torno do eixo oy.
Solução:
Fazendo o esboço da região R:
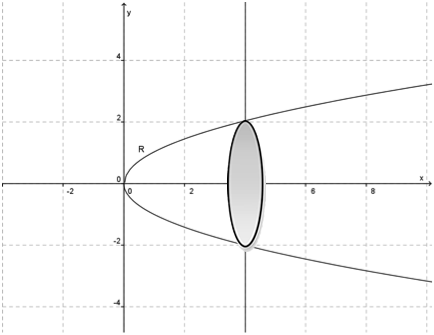
Calculando o volume:
