Operações com Vetores na Forma Analítica
Vetores no Plano:
Qualquer vetor não nulo pode ser expresso em função de dois vetores não paralelos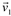 
e 
.
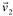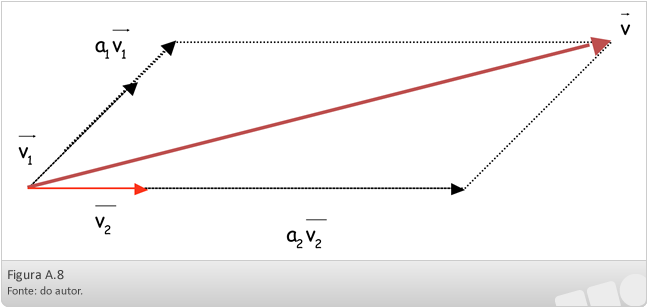
E neste caso dizemos que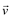 
é combinação linear d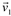e e .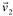
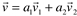
Também dizemos que conjunto desses vetores:
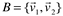Forma uma base do 
.
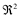As bases mais utilizadas são as ortonormais àquelas em que os vetores são ortogonais e unitários.
Os vetores nesse sistema são representados por e
, ambos com origem na origem dos eixos coordenados e extremidade em (1 , 0) e (1 , 0) respectivamente.
A base mais utilizada é chamada de base canônica:
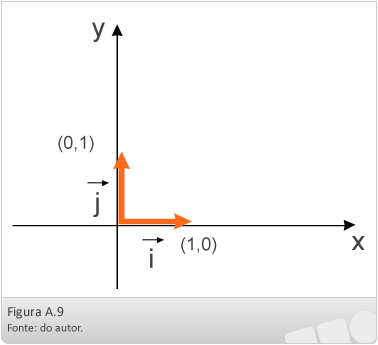
Usando a base canônica determinamos a expressão analítica de um vetor:
Ou seja, tomando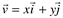 
Escrevemos o vetor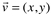 
portanto um vetor é um ponto do plano.
Exemplos:
| Forma canÔnica | Forma analÍtica |
 |
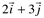(2,3) |
 |
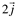(0,2) |
 |
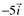(-5,0) |
 |
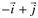(-1,1) |