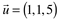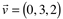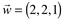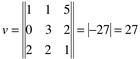Produto Entre Vetores
Produto Escalar
Chama-se produto escalar de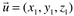 
e 
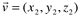ao número real 
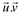dado por:
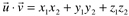
Exemplo:
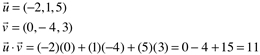
Aplicações do produto escalar
Uma aplicação importante do produto escalar é a condição de ortogonalidade entre vetores:
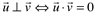
Exemplo:
Os vetores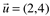 
e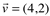 
são ortogonais, pois fazendo o produto escalar o resultado é zero.
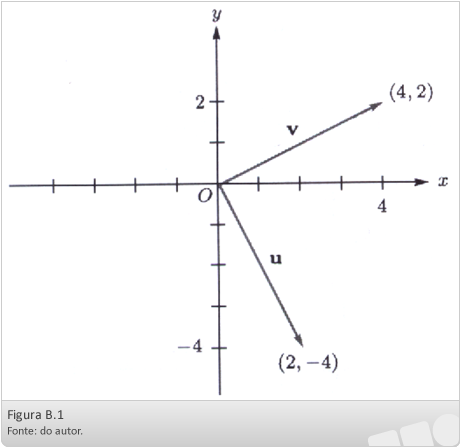
Outra aplicação importante é o cálculo do ângulo entre dois vetores:
A fórmula é dada por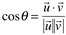 
Exemplo:
Calcular o ângulo entre os vetores:
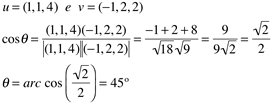
Produto Vetorial
O produto vetorial de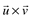 
é o vetor de módulo igual à área do paralelogramo definido pelos dois vetores e direção perpendicular ao plano do paralelogramo.
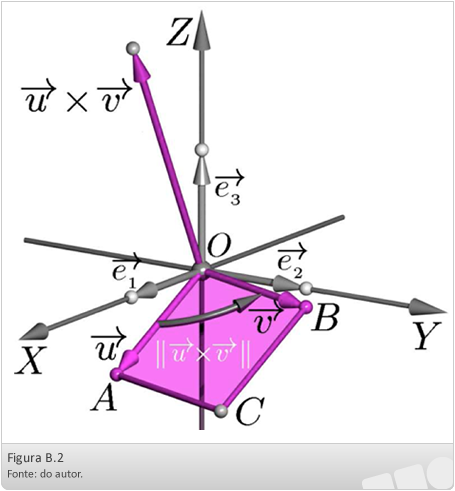
Para facilitar o cálculo desse produto vetorial, utilizaremos a seguinte notação:
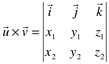
Exemplo:
Dados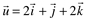 
e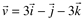 
determine u vetorial v:
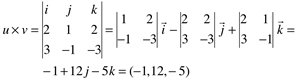
A interpretação geométrica do módulo do produto vetorial é numericamente igual à área do paralelogramo formado por esses vetores:
Produto Misto
Dados os vetores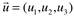 
,
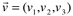e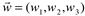 
definimos o produto misto entre u, v e w, denotado por [u,v,w] ou por u.(v×w), como o número real obtido a partir do determinante
[u,v,w] = u·(v×w) =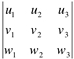 
O resultado do produto misto é um NÚMERO REAL.
Exemplo:
Dados os vetores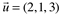 
,
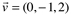e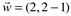 
calcule o produto misto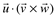 
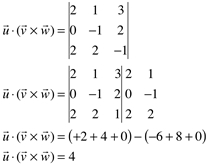
A interpretação geométrica do módulo do produto misto é numericamente igual ao volume do paralelepípedo definido pelos vetores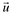 
,
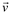e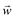 
.
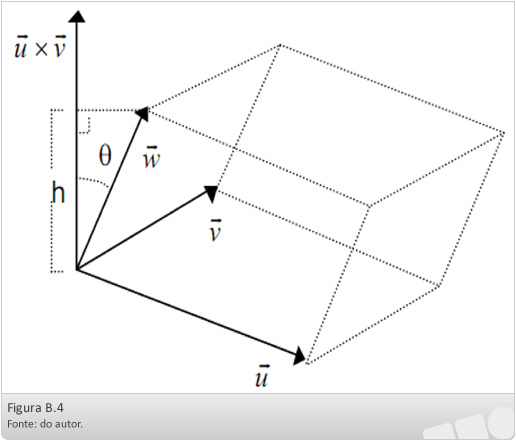
V = | (u,v,w) |
Exemplo
Calcule o volume do paralelepípedo formado pelos vetores:
