Funções de Várias Variáveis
Todas aquelas regras válidas para as quantidades escalares são válidas para as quantidades vetoriais.
O conceito de derivada parcial pode ser aplicado geometricamente para encontrar a inclinação de uma superfície na direção de x e y.
Podemos aplicar as derivadas parciais como taxa de variação e essa interpretação envolve muitos fenômenos físicos.
Definições
Função de Duas Variáveis
Uma função real f de duas variáveis é uma relação que a cada par ordenado de números reais (x, y) associa um único número real z=f (x, y).

As funções de duas variáveis aparecem em muitas situações práticas, tais como:
Áreas de figuras que dependem da altura e da largura.
Volumes que dependem da altura e do raio.
Representações
As funções de duas variáveis podem ser representadas graficamente por superfícies em sistema tridimensional de coordenadas.
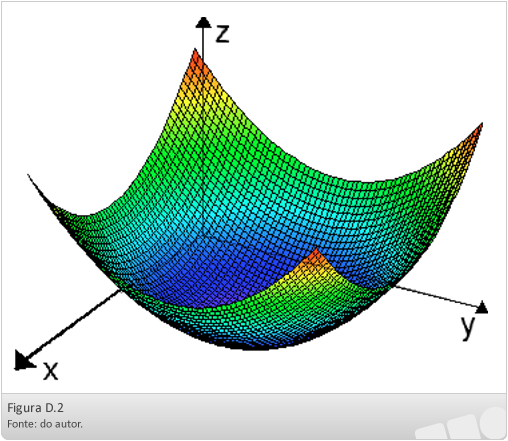
Alguns gráficos de funções de duas variáveis:
| EquaÇÃo | SuperfÍcie gerada | exemplo |
| z = ax + by + c | Plano. | 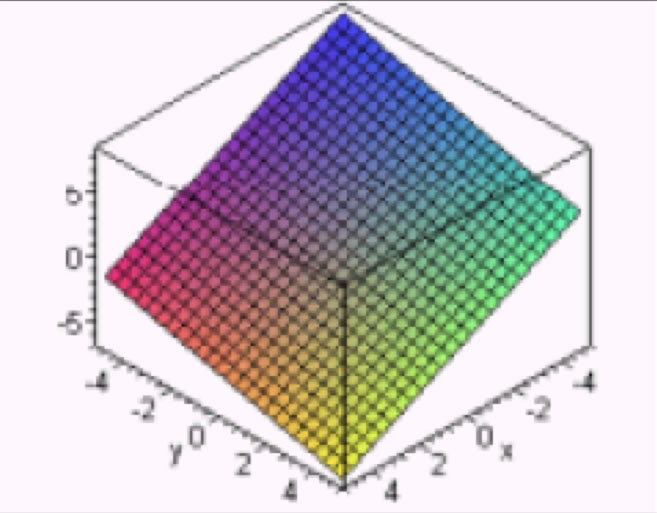 |
| z = ax2 + by2 + c | Paraboloide Elíptico. | 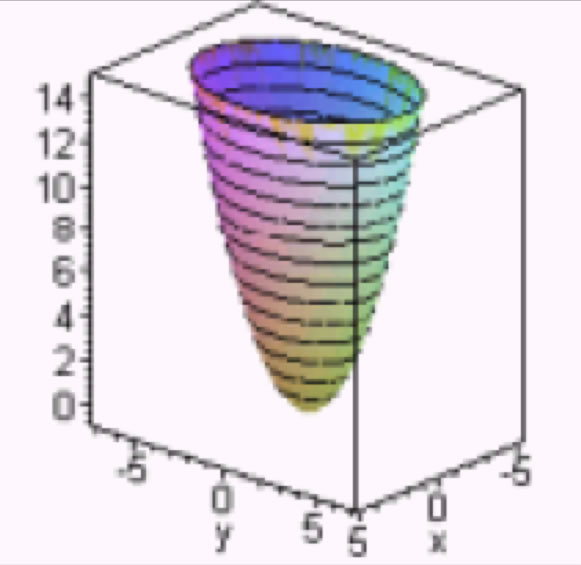 |
Características
Podemos classificar as funções de duas variáveis em explícitas ou implícitas
Explícitas
Podem ser colocadas na forma : 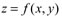
Implícitas
Podem ser colocadas na forma: 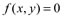
Funções de várias variáveis
Definição: Diz-se que z é uma função de x, y,...,t, e escreve-se z=f(x,y,....t), quando a correspondência entre z e o conjunto (x, y, ...,t) é tal que para cada grupo (xi, yi,....,ti) o valor de zi fique univocamente definido.

Domínio de f(x,y,....t): é o conjunto de todos os valores (x,y, ...t) possíveis para as variáveis independentes.
Exemplo:
Determine o domínio da função abaixo e represente-o graficamente
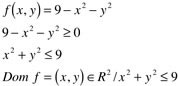
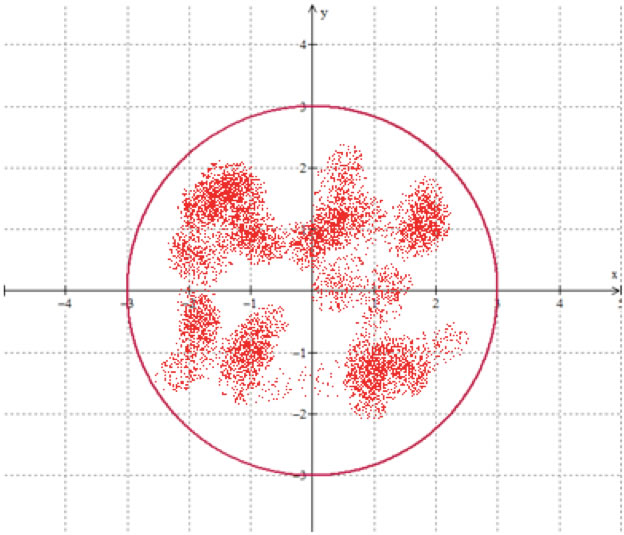
Limites de Funções de duas Variáveis
Dada uma função f(x,y), dizemos que o limite de f é igual a L quando (x,y) se aproxima de um ponto de referência (a,b), se pudermos tornar os valores de f(x,y) tão próximos de L conforme (x,y) se aproximar de (a,b).
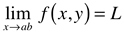
Para se estimar o limite de uma função de duas variáveis f no ponto (x0, y0) é necessário calcular esse valor por todas as trajetórias que passem por este ponto. Se em todos os casos o resultado for sempre o mesmo, digamos L, diz-se que o limite existe e que vale L.
Caso o limite não exista em alguma trajetória ou dê um valor diferente para trajetórias diferentes, dizemos que o limite não existe.
Exemplo
Mostre que a função abaixo não tem limite quando (x,y) se aproxima de (0,0).
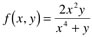
Tentamos calcular o limite por substituição direta, o que gera a indeterminação 0/0.
Tomamos uma trajetória que passe pelo ponto (0,0), y=kx².
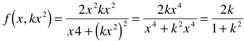
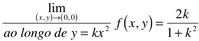
Note que este limite varia de acordo com o valor escolhido para k. Logo, este limite não existe.
Continuidade
