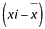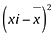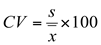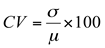Medidas de dispersão ou de variabilidade
Amplitude total
A amplitude total (AT), ou range, em um conjunto de dados é a diferença entre o maior e o menor valor observado.
Assim, podemos estabelecer que: AT = x(máx.) – x (mín.)
Tomando por exemplo os seguintes dados amostrais:
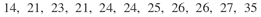
Calculamos a amplitude total como:
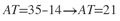
Podemos perceber que a amplitude total considera apenas o valor máximo e o valor mínimo, não importando todos os demais valores do conjunto de dados. Esta condição tem o inconveniente de expor a medida de amplitude total à presença de valores extremos ou atípicos, chamados outliers, o que quase sempre invalida a idoneidade do resultado (CRESPO, 2009).
Assim, devemos aperfeiçoar a descrição da variabilidade dos dados através de outras medidas de dispersão, como a variância ou o desvio padrão.
Variância
A variância (s2) e o desvio padrão levam em consideração a totalidade dos valores assumidos pela variável em estudo, e assim, são índices de variabilidade bastante estáveis e geralmente os mais empregados. A variância expressa a média aritmética dos quadrados dos desvios. Definimos desvio como sendo a diferença entre um determinado valor da variável em estudo e a média dos valores totais.
Assim, a variância de uma população será calculada por:
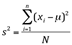
Onde:
xi = valor de ordem i assumido pela variável
µ = média dos valores de x
s² = variância populacional
N = número de dados da população
Se os dados que estamos avaliando é uma amostra da população total de dados então a variância calculada é denominada variância amostral, e será calculada pela seguinte fórmula:
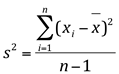
A diferença de cálculo entre as fórmulas está no denominador. O somatório dos quadrados dos desvios foi dividido por n-1 em lugar de N, porque proporciona uma melhor estimativa da variância populacional e porque, sendo nula a soma dos desvios, existem (n – 1) desvios independentes, e assim, conhecidos (n – 1) desvios o último está automaticamente determinado, pois a soma é zero.
 |  | |
|
Embora o processo de cálculo da média aritmética seja o mesmo para um conjunto de dados que representem uma amostra da população ou para todos os dados que compõem a população, utiliza-se o símbolo µ para representar a média da população, e N para o número de elementos da população. | ||
 |  |
Considerando os mesmo dados com os quais calculamos a amplitude total, vamos ver como obtemos os desvios e a variância dos dados, demonstrados na Tabela 1.
Tabela 1 – Cálculo dos desvios para obtenção da variância.
Ordem |
Dados |
Desvio |
Desvio2 |
1 |
14 |
-10,182 |
103,673 |
2 |
21 |
-3,182 |
10,125 |
3 |
21 |
-3,182 |
10,125 |
4 |
23 |
-1,182 |
1,397 |
5 |
24 |
-0,182 |
0,033 |
6 |
24 |
-0,182 |
0,033 |
7 |
25 |
0,818 |
0,669 |
8 |
26 |
1,818 |
3,305 |
9 |
26 |
1,818 |
3,305 |
10 |
27 |
2,818 |
7,941 |
11 |
35 |
10,818 |
117,029 |
n=11 |
∑= 266 |
|
∑= 254,33 |
A média será:
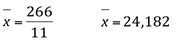
E a variância amostral:
s2= 254,33 / 10 → s2 = 25,43 |
Quando a média não é exata e tem de ser arredondada, cada desvio fica ligeiramente afetado pelo erro devido ao arredondamento. O mesmo irá acontecer com os quadrados dos desvios. Uma fórmula alternativa, bastante usada para o cálculo da variância amostral, é:
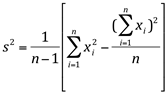
Se estivermos calculando a variância populacional, substituímos 1/n-1 por 1/N.
Recalculando a variância dos dados apresentados na Tabela 1, através da fórmula alternativa, temos:
Tabela 2 – Cálculo da variância pela fórmula alternativa.
Ordem |
(xi) |
(xi)² |
1 |
14 |
196 |
2 |
21 |
441 |
3 |
21 |
441 |
4 |
23 |
529 |
5 |
24 |
576 |
6 |
24 |
576 |
7 |
25 |
625 |
8 |
26 |
676 |
9 |
26 |
676 |
10 |
27 |
729 |
11 |
35 |
1225 |
n=11 |
∑xi= 266 |
∑xi²=6.690 |
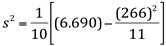
E o novo valor da variância será:
s² = 25,76 |
A diferença é devido ao arredondamento da média, como descrito anteriormente.
Se os desvios em relação à media são pequenos, podemos concluir que as observações estão aglomeradas em torno da média e a variabilidade dos dados é pequena. Por sua vez, se os desvios são grandes, os dados estão muito dispersos e a variabilidade é grande. A variância tem a capacidade de captar essas duas situações, portanto é um bom índice estimador da variabilidade dos dados.
Como a variância é calculada a partir dos quadrados dos desvios, seu resultado é um número em unidade quadrada em relação à variável sob estudo, o que, sob o ponto de vista prático, é um inconveniente. Como exemplo, vamos assumir que os dados apresentados na Tabela 2 representassem dias de ocorrência de geada nos últimos onze anos em Pelotas (dados fictícios). A variância então assume o valor de 25,76 dias².
Se extrairmos a raiz quadrada da variância, teremos uma medida da variabilidade dos dados e os próprios dados na mesma unidade. Esse novo índice de variabilidade é o que definimos como desvio padrão.
Desvio padrão
O desvio padrão (s ou σ) é definido como sendo a raiz quadrada da média aritmética dos quadrados dos desvios e, dessa forma, é dado pela raiz quadrada da variância.
A equação para o cálculo do desvio padrão amostral é:
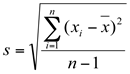
E para o desvio padrão populacional:
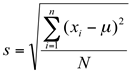
Quando o desvio padrão é calculado usando todos os elementos da população é simbolizado pela letra grega σ (sigma), denominado desvio padrão populacional, sendo considerado um parâmetro.
Se for calculado a partir de uma amostra da população, é representado pela letra s, denominado desvio padrão amostral, e é considerado um estimador.
O desvio padrão dos dados apresentados na Tabela 2 será:
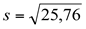onde: s = 5,07 dias
Tanto o desvio padrão como a variância são usados como medidas de dispersão ou variabilidade. O uso de uma ou de outra dependerá da finalidade que se tenha em vista. A variância é uma medida que tem pouca utilidade como estatística descritiva, porém é extremamente importante na inferência estatística e em combinações de amostras (CRESPO, 2009).
Coeficiente de variação
O coeficiente de variação (CV) é uma medida de variabilidade relativa que mede a dispersão dos dados em relação à média aritmética, sendo expressa pela razão entre o desvio padrão e a média, e multiplicada por cem. Assim, é uma medida adimensional expressa em percentual.
Tipo |
RepresentaÇÃo |
unidade |
CV amostral |
|
% |
CV populacional |
|
% |
Exemplo:
Considere amostragens realizadas em duas escolas, com relação às notas obtidas por alunos da disciplina de estatística na primeira avaliação.
Medida |
Escola A |
Escola B |
Média |
6,5 |
6,5 |
Variância |
1,167 |
0,416 |
Desvio Padrão |
1,08 |
0,64 |
CV % |
16,61 |
9,93 |
Embora o valor das médias tenha a mesma magnitude, é possível perceber que a Escola B apresenta menor dispersão dos dados, demonstrado nos menores valores de variância, desvio padrão e coeficiente de variação. O que está indicando que os alunos da escola B tiveram um desempenho mais homogêneo, com os dados variando menos em relação à média (menores desvios). Apesar de, no exemplo apresentado, a avaliação parecer um tanto óbvia, existem situações em que a magnitude dos valores das variáveis que se está comparando são diferentes e a conclusão a respeito dos dados é dificultada quando apenas a média e o desvio padrão são apresentados. O coeficiente de variação é a medida mais utilizada quando existe interesse em comparar variabilidade de diferentes conjuntos de dados.
Medidas separatrizes
Pelo que apresentamos na aula anterior, relativo às medidas de posição, e nessa aula com relação às medidas de dispersão, podemos concluir que tanto a média como o desvio padrão são afetados por valores extremos. Assim, quando a distribuição dos dados não é simétrica, ou seja, os dados não se distribuem de forma homogênea ao redor da média, temos uma distribuição assimétrica e precisamos conhecer outras medidas que permitam uma boa caracterização do conjunto de dados.
As medidas separatrizes, embora não sejam consideradas individualmente como medidas de tendência central, são baseadas em sua posição na série de dados. Assim, os quartis, os percentis e os decis, juntamente com a mediana, são medidas conhecidas como separatrizes.
Quartis
Os quartis são os valores de uma série de dados que a dividem em quatro partes iguais. Assim, os quartís Q1, Q2 e Q3, dividem os dados em quatro partes, de tal forma que cada parte possui 25% dos dados, ou um quarto (1/4), daí sua denominação.
O primeiro quartil (Q1) separa os dados de maneira que 25% dos valores são inferiores ou igual ao Q1 e 75% dos dados são superiores ou igual ao Q1.
Consideremos os seguintes dados:
5 |
5,5 |
6 |
7,0 |
7,5 |
8,5 |
9,5 |
11 |
Q1 |
Q2 |
Q3 |
|||||
25% |
50% |
75% |
100% |
||||
Na representação gráfica dos quartis podemos perceber que, o primeiro quartil situa-se entre os valores de 5,5 e 6, o segundo quartil entre os valores de 7,0 e 7,5, e é coincidente com a mediana, e o terceiro quartil situa-se entre os valores de 8,5 e 9,5.
Para calcular a posição dos quartis utilizamos a seguinte relação:
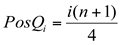
Assim, para os dados apresentados, o Q2 será:
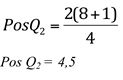
Interpretando o resultado: Significa que o segundo quartil equivale ao valor da posição 4,5, ou seja, intermediária entre a 4ª e a 5ª posição. Precisamos então fazer a média entre os valores da quarta e da quinta posição, 7,0 e 7,5, respectivamente. O valor de Q2 será 7,25 e significa que, 50% dos valores são inferiores ou iguais a 7,25 e 50% dos valores são iguais ou superiores a 7,25. Observe que o valor de Q2 coincide com o valor da mediana.
Amplitude interquartílica
A amplitude interquartílica, denotada por q, é a diferença entre o terceiro quartil (Q3) e o primeiro quartil (Q1). Assim temos:
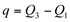
Apesar de ser uma medida pouca utilizada, a amplitude interquartílica apresenta uma característica interessante que é a resistência, ou seja, esta medida, ao contrário da amplitude total, não sofre nenhuma influência de valores discrepantes.
Percentis
Os percentis dividem a série de dados em cem partes iguais, cada uma com 1%, de tal maneira que o P50 corresponde ao Q2 e a mediana.
Para determinar a posição dos percentis utilizamos a seguinte relação:
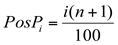
Assim, o P50 será:
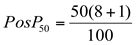
Pos P50 = 4,5 (que é igual ao Q2 calculado).