Medidas de Assimetria
Uma distribuição é dita simétrica quando a média, a mediana e a moda são coincidentes. Assim, em uma distribuição simétrica, o gráfico que representa a distribuição dos valores e sua frequência tem a forma de sino, conforme a figura 1.
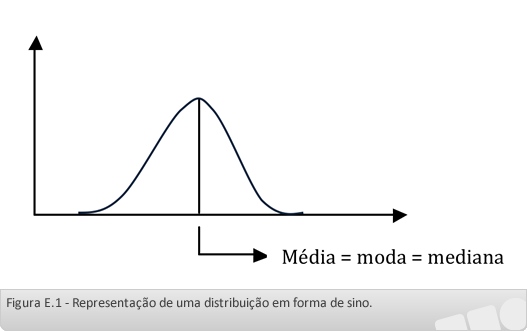
A partir da figura podemos observar que os dados apresentam o mesmo comportamento, ou distribuição, à direita e a esquerda da média e nesse caso, a média, a moda e a mediana são iguais ou muito próximas.
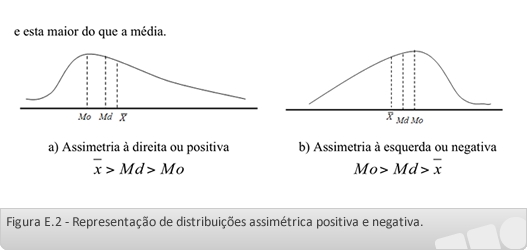
A assimetria é dita positiva (Figura 2-a) quando a cauda direita afasta-se mais do pico do que a cauda esquerda, e assim, a média é maior do que a mediana, a qual é maior do que a moda.
A distribuição de dados apresenta assimetria negativa (Figura 2-b) quando sua cauda esquerda afasta-se mais do pico do que a cauda direita, e nesse caso, a moda é maior do que a mediana, e esta maior do que a média.
Há mais de uma forma para determinação da assimetria, sendo que a determinação pelo segundo critério de Pearson, ou coeficiente de assimetria de Pearson, é dada por:
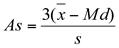
Onde: As = coeficiente de assimetria de Pearson
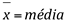
Md = mediana
S = desvio padrão
O coeficiente de assimetria de Pearson tem as seguintes interpretações:
As ≤ -1 |
Assimetria negativa |
-1 < As < -0,15 |
Assimetria negativa moderada |
-0,15 ≤ As ≤ +0,15 |
Simétrica |
+0,15 < As < +1 |
Assimetria positiva moderada |
As ≥ +1 |
Assimetria positiva |