Grau de Curtose
Denominamos de curtose o grau de achatamento ou alongamento da curva característica do conjunto de dados ou distribuição em relação a uma distribuição padrão, denominada curva normal.
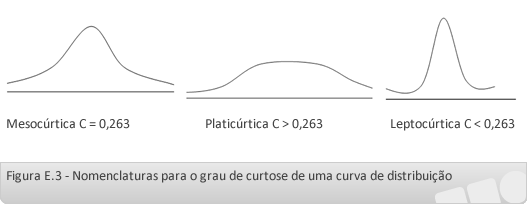
A curva normal recebe o nome de mesocúrtica (Figura 3) e possui coeficiente de curtose (C ) igual a 0,263.
Se uma curva é mais fechada que a normal (apresentando-se pontiaguda em sua parte superior), ela é chamada de leptocúrtica e possui coeficiente de curtose inferior a 0,263.
Se a curva apresentar um achatamento maior do que a curva normal, ela é chamada de platicúrtica e apresenta coeficiente de curtose maior do que 0,263.
Uma fórmula utilizada para o cálculo do coeficiente de curtose (C), conhecida como coeficiente percentílico de curtose, é apresentada a seguir:
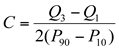
Onde:
C = Coeficiente de Curtose;
Q3 e Q1 = quartil 3 e quartil 1, respectivamente;
P90 e P10 = percentil 90 e percentil 10, respectivamente.
Exercício resolvido:
1- Os resultados de 20 leituras de temperatura medidas no efluente da etapa de despolpa no processo de fabricação de pêssego em calda, são apresentados a seguir:
17,0 |
17,5 |
17,5 |
18,0 |
18,2 |
18,2 |
18,5 |
18,5 |
18,9 |
18,9 |
18,9 |
18,9 |
20,9 |
20,9 |
20,9 |
23,5 |
23,5 |
24,6 |
24,7 |
25,5 |
Calcule:
a) a média amostral
b) a amplitude total
c) a variância
d) o desvio padrão
e) o coeficiente de variação
f) a amplitude interquartílica
g) o coeficiente de assimetria e a classificação da assimetria
h) o coeficiente de curtose e a classificação da curtose
Respostas:
Organizando os dados em uma tabela, temos:
Ordem |
(xi) |
(xi)² |
1 |
17,0 |
289,00 |
2 |
17,5 |
306,25 |
3 |
17,5 |
306,25 |
4 |
18,0 |
324,00 |
5 |
18,2 |
331,24 |
6 |
18,2 |
331,24 |
7 |
18,5 |
342,25 |
8 |
18,5 |
342,25 |
9 |
18,9 |
357,21 |
10 |
18,9 |
357,21 |
11 |
18,9 |
357,21 |
12 |
18,9 |
357,21 |
13 |
20,9 |
436,81 |
14 |
20,9 |
436,81 |
15 |
20,9 |
436,81 |
16 |
23,5 |
552,25 |
17 |
23,5 |
552,25 |
18 |
24,6 |
605,16 |
19 |
24,7 |
610,09 |
20 |
25,5 |
650,25 |
n=20 |
∑= 403,50 |
∑= 8281,75 |
a) a média será:
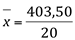
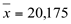
b) a amplitude total será:
AT = 25,5 – 17,0 
AT=8,5
c) a variância:
usando a fórmula: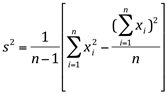 
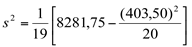s²=7,43
d) desvio padrão:
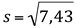
s = 2,725
e) coeficiente de variação:
CV = (2,725 / 20,175) x 100
CV = 13,51%
f) amplitude interquartílica (q):
q = Q3-Q1
PosQ3= [3(20+1)] / 4
PosQ3= 15,75
Pos15 = 20,9 e Pos16 = 23,5 logo, Pos15,75= 22,85 e Q3=22,85
PosQ1= [1(20+1)]/4
PosQ1= 5,25
Pos5=18,2 e Pos6=18,2 logo, Pos5,25= 18,2 e Q1=18,2
q= 22,85 – 18,2
q = 4,65
g) o coeficiente de assimetria e a classificação da assimetria
- para calcular o coeficiente de assimetria temos que conhecer o valor da mediana (Md):
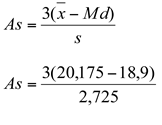
As = 1,40 à assimetria positiva |
h) o coeficiente de curtose e a classificação da curtose
- para calcular o coeficiente de curtose (C), precisamos antes calcular P90 e P10 :
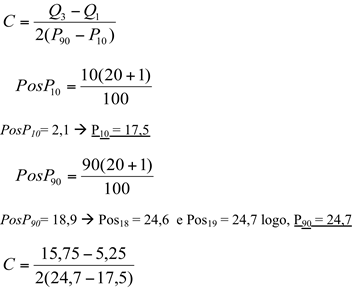
C = 0,729 → platicúrtica (C > 0,263)
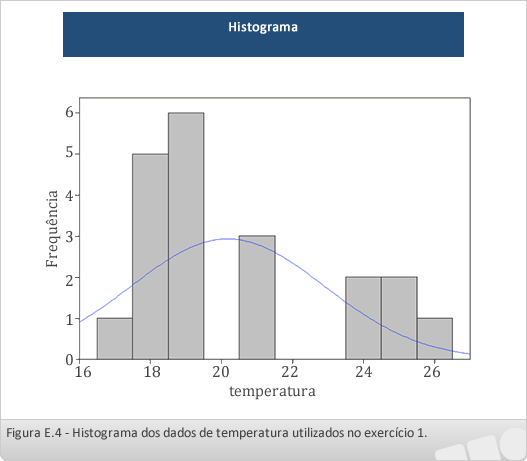
Na Figura 4 é apresentado o histograma dos dados de temperatura utilizados no exercício. Podemos observar a assimetria, com a cauda direita afastando-se mais do pico do que a cauda esquerda, e assim, a média (20,175) é maior do que a mediana (18,9) e do que a moda (18,9).
Podemos observar também, o maior achatamento da curva de distribuição dos dados em relação à curva normal, (platicúrtica) com coeficiente de curtose maior do que 0,263.
