Distribuição binomial
Um experimento binomial tem as seguintes características:
- As n tentativas de um mesmo experimento são independentes, ou seja, o resultado de uma tentativa não afeta os resultados das sucessivas;
- Cada tentativa admite apenas dois resultados: sucesso ou fracasso, acertar ou errar, cara ou coroa, entre outros;
- No decorrer do experimento, a probabilidade p do sucesso e a probabilidade q do fracasso (q= 1- p ) permanecem constantes.
Logo, se em n tentativas independentes de um experimento em que o resultado esperado só poderá ser p ou q (sucesso ou fracasso, respectivamente), e a probabilidade p for constante em todo o experimento, então a probabilidade de a variável aleatória x ter k (número de sucessos) nas n tentativas será obtida por:
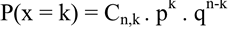
Onde:
P(x = k) é a probabilidade de que o evento se realize k vezes em n provas;
p é a probabilidade de que o evento se realize em uma só prova (sucesso);
q é a probabilidade de que o evento não se realize em uma só prova (fracasso);
Cn,k é o coeficiente binomial de n sobre k, igual a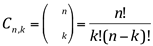 
 |  | |
|
n! é o fatorial de n, por exemplo, se n=3, n! = 3x2x1. | ||
 |  |
Essa função, denominada lei binomial, define a distribuição binomial.
| | |
|
Segundo CRESPO (2009), o nome binomial vem do fato de que
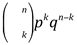é o termo geral de desenvolvimento do binômio de Newton.
| ||
| |
Exemplo de aplicação:
Determine a probabilidade de ocorrer exatamente duas coroas no conjunto de dez lançamentos de uma moeda.
x= número de coroas
n = 10
p = 0,5
q= 0,5
k= 2
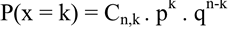
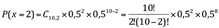
P(x = 2) = 45 x 0,25 x 0,0039
P(x = 2) =0,0439
Multiplicando o resultado por 100, obtemos a probabilidade em porcentagem:
P(x = 2) =4,39%