Distribuição normal
Entre as distribuições teóricas de variável aleatória contínua, uma das mais empregadas é a distribuição normal. Uma das propriedades das distribuições normais é a simetria da curva, como pode ser visto na Figura 1.
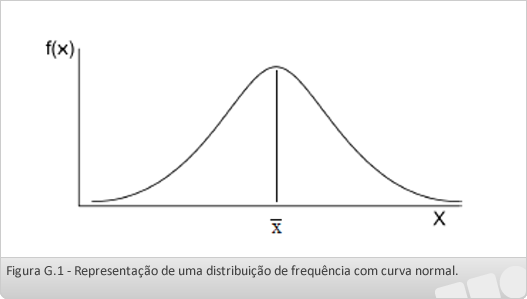
Figura 1 – Representação de uma distribuição de frequência com curva normal.
Características da curva normal:
- A curva é simétrica em relação à média µ (x barra);
- A variável aleatória x pode assumir todo e qualquer valor real;
- A representação gráfica da distribuição normal é uma curva em forma de sino, simétrica em torno da média, que recebe o nome de curva normal ou de Gauss;
- A área total delimitada pela curva e pelo eixo das abscissas é 1 ou 100%;
- A curva normal é assintótica em relação ao eixo das abscissas, isto é, aproxima-se indefinidamente do eixo das abscissas sem, contudo, alcançá-lo;
- Como a curva é simétrica em torno da média, a probabilidade de ocorrer valor maior do que a média é igual a probabilidade de ocorrer valor menor do que a média, isto é :
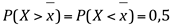
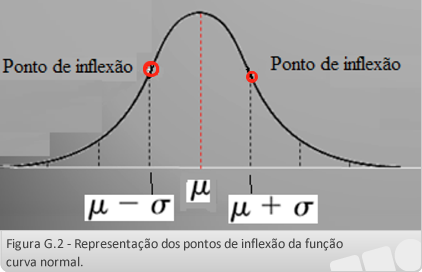
- Os pontos de inflexão da função são µ-σ e µ+σ :
Assim, quando trabalhamos com uma variável aleatória com distribuição normal, podemos obter a probabilidade de essa variável aleatória assumir um valor em um determinado intervalo. Para tanto, a fórmula para obter essa probabilidade é:
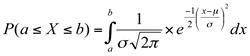
Para utilizar essa função é necessária a aplicação de integração numérica, o que seria muito trabalhoso e exigiria conhecimentos que não serão tratados em nossas aulas. Entretanto, podemos contornar facilmente esse problema utilizando a variável normal padrão ou variável padronizada, z.
A variável padronizada z tem distribuição normal reduzida, ou seja, tem distribuição normal de média igual a zero e desvio padrão igual a um.
Sendo x uma variável aleatória com distribuição normal de média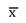 
e desvio padrão s, a variável padronizada z será dada por:
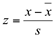
As probabilidades associadas à distribuição normal padronizada não precisam ser calculadas, sendo encontradas em tabelas. A Tabela 3 apresenta a Distribuição Normal Padrão, com os valores calculados para a probabilidade p de valores entre a média zero e o valor Zc.
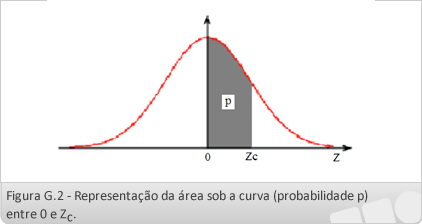
Tabela 3 - Distribuição Normal Padrão (probabilidade p, tal que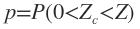 
Zc |
Segundo decimal de Zc |
|||||||||
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
|
0.0 |
0.0000 |
0.0040 |
0.0080 |
0.0120 |
0.0160 |
0.0199 |
0.0239 |
0.0279 |
0.0319 |
0.0359 |
0.1 |
0.0398 |
0.0438 |
0.0478 |
0.0517 |
0.0557 |
0.0596 |
0.0636 |
0.0675 |
0.0714 |
0.0753 |
0.2 |
0.0793 |
0.0832 |
0.0871 |
0.0910 |
0.0948 |
0.0987 |
0.1026 |
0.1064 |
0.1103 |
0.1141 |
0.3 |
0.1179 |
0.1217 |
0.1255 |
0.1293 |
0.1331 |
0.1368 |
0.1406 |
0.1443 |
0.1480 |
0.1517 |
0.4 |
0.1554 |
0.1591 |
0.1628 |
0.1664 |
0.1700 |
0.1736 |
0.1772 |
0.1808 |
0.1844 |
0.1879 |
0.5 |
0.1915 |
0.1950 |
0.1985 |
0.2019 |
0.2054 |
0.2088 |
0.2123 |
0.2157 |
0.2190 |
0.2224 |
0.6 |
0.2257 |
0.2291 |
0.2324 |
0.2357 |
0.2389 |
0.2422 |
0.2454 |
0.2486 |
0.2517 |
0.2549 |
0.7 |
0.2580 |
0.2611 |
0.2642 |
0.2673 |
0.2704 |
0.2734 |
0.2764 |
0.2794 |
0.2823 |
0.2852 |
0.8 |
0.2881 |
0.2910 |
0.2939 |
0.2967 |
0.2995 |
0.3023 |
0.3051 |
0.3078 |
0.3106 |
0.3133 |
0.9 |
0.3159 |
0.3186 |
0.3212 |
0.3238 |
0.3264 |
0.3289 |
0.3315 |
0.3340 |
0.3365 |
0.3389 |
1.0 |
0.3413 |
0.3438 |
0.3461 |
0.3485 |
0.3508 |
0.3531 |
0.3554 |
0.3577 |
0.3599 |
0.3621 |
1.1 |
0.3643 |
0.3665 |
0.3686 |
0.3708 |
0.3729 |
0.3749 |
0.3770 |
0.3790 |
0.3810 |
0.3830 |
1.2 |
0.3849 |
0.3869 |
0.3888 |
0.3907 |
0.3925 |
0.3944 |
0.3962 |
0.3980 |
0.3997 |
0.4015 |
1.3 |
0.4032 |
0.4049 |
0.4066 |
0.4082 |
0.4099 |
0.4115 |
0.4131 |
0.4147 |
0.4162 |
0.4177 |
1.4 |
0.4192 |
0.4207 |
0.4222 |
0.4236 |
0.4251 |
0.4265 |
0.4279 |
0.4292 |
0.4306 |
0.4319 |
1.5 |
0.4332 |
0.4345 |
0.4357 |
0.4370 |
0.4382 |
0.4394 |
0.4406 |
0.4418 |
0.4429 |
0.4441 |
1.6 |
0.4452 |
0.4463 |
0.4474 |
0.4484 |
0.4495 |
0.4505 |
0.4515 |
0.4525 |
0.4535 |
0.4545 |
1.7 |
0.4554 |
0.4564 |
0.4573 |
0.4582 |
0.4591 |
0.4599 |
0.4608 |
0.4616 |
0.4625 |
0.4633 |
1.8 |
0.4641 |
0.4649 |
0.4656 |
0.4664 |
0.4671 |
0.4678 |
0.4686 |
0.4693 |
0.4699 |
0.4706 |
1.9 |
0.4713 |
0.4719 |
0.4726 |
0.4732 |
0.4738 |
0.4744 |
0.4750 |
0.4756 |
0.4761 |
0.4767 |
2.0 |
0.4772 |
0.4778 |
0.4783 |
0.4788 |
0.4793 |
0.4798 |
0.4803 |
0.4808 |
0.4812 |
0.4817 |
2.1 |
0.4821 |
0.4826 |
0.4830 |
0.4834 |
0.4838 |
0.4842 |
0.4846 |
0.4850 |
0.4854 |
0.4857 |
2.2 |
0.4861 |
0.4864 |
0.4868 |
0.4871 |
0.4875 |
0.4878 |
0.4881 |
0.4884 |
0.4887 |
0.4890 |
2.3 |
0.4893 |
0.4896 |
0.4898 |
0.4901 |
0.4904 |
0.4906 |
0.4909 |
0.4911 |
0.4913 |
0.4916 |
2.4 |
0.4918 |
0.4920 |
0.4922 |
0.4925 |
0.4927 |
0.4929 |
0.4931 |
0.4932 |
0.4934 |
0.4936 |
2.5 |
0.4938 |
0.4940 |
0.4941 |
0.4943 |
0.4945 |
0.4946 |
0.4948 |
0.4949 |
0.4951 |
0.4952 |
2.6 |
0.4953 |
0.4955 |
0.4956 |
0.4957 |
0.4959 |
0.4960 |
0.4961 |
0.4962 |
0.4963 |
0.4964 |
2.7 |
0.4965 |
0.4966 |
0.4967 |
0.4968 |
0.4969 |
0.4970 |
0.4971 |
0.4972 |
0.4973 |
0.4974 |
2.8 |
0.4974 |
0.4975 |
0.4976 |
0.4977 |
0.4977 |
0.4978 |
0.4979 |
0.4979 |
0.4980 |
0.4981 |
2.9 |
0.4981 |
0.4982 |
0.4982 |
0.4983 |
0.4984 |
0.4984 |
0.4985 |
0.4985 |
0.4986 |
0.4986 |
3.0 |
0.4987 |
0.4987 |
0.4987 |
0.4988 |
0.4988 |
0.4989 |
0.4989 |
0.4989 |
0.4990 |
0.4990 |
3.1 |
0.4990 |
0.4991 |
0.4991 |
0.4991 |
0.4992 |
0.4992 |
0.4992 |
0.4992 |
0.4993 |
0.4993 |
3.2 |
0.4993 |
0.4993 |
0.4994 |
0.4994 |
0.4994 |
0.4994 |
0.4994 |
0.4995 |
0.4995 |
0.4995 |
3.3 |
0.4995 |
0.4995 |
0.4995 |
0.4996 |
0.4996 |
0.4996 |
0.4996 |
0.4996 |
0.4996 |
0.4997 |
3.4 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4997 |
0.4998 |
3.5 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
0.4998 |
3.6 |
0.4998 |
0.4998 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
3.7 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
3.8 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
0.4999 |
3.9 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
0.5000 |
Exemplo de aplicação da tabela da curva normal padrão:
Para usar a Tabela 3, da curva normal padrão, devemos considerar o fato de que a curva é simétrica e centrada na média. No corpo da Tabela estão os valores das probabilidades (área sob a curva entre os limites de zero e Zc). Os valores de Zc estão na margem esquerda e na margem superior da tabela, de tal forma que, na margem esquerda (primeira coluna) aparece o valor inteiro e a primeira casa decimal de Zc, enquanto na primeira linha aparece o valor do segundo decimal de Zc.
Consideremos o seguinte exemplo: Seja X a variável aleatória que representa o comprimento de determinada peça produzida por uma máquina, a qual tem distribuição normal de média igual a 2,0 cm e desvio padrão de 0,20cm. Precisamos conhecer a probabilidade de que uma peça produzida tenha comprimento entre 2,0 cm (a média) e 2,15 cm.
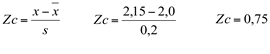
Para obter o valor de Zc=0,75 basta que, na primeira coluna, localizemos o valor de 0,7 e na intersecção da linha que contém o valor de 0,7 com a coluna que contém o valor 0,05 encontraremos o valor de p= 0,2734 que corresponde a Zc=0,75, conforme ilustrado abaixo.
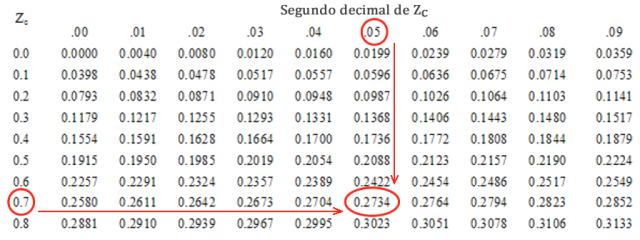
O valor 0,2734 corresponde a probabilidade de que uma peça produzida tenha dimensão entre a média (2,0cm) e 2,15cm, ou seja, 27,34% de probabilidade.
Observe que no exemplo apresentado, o valor do limite inferior de medida do parafuso coincide com o valor da média e, portanto, o valor de Zc para essa medida é zero, o que resulta em 0,2734 – 0 = 0,2734.
Se os valores procurados fossem entre 2,05cm e 2,15cm, teríamos que calcular o valor de Zc para 2,05cm, que resultaria em 0,25. Entrando com o valor de 0,25 na tabela iremos obter o valor de 0,097 para a probabilidade p. Assim, para essa faixa de valores, a probabilidade seria:
P(2,05≤ X ≤ 2,15) = 0,2734 – 0,097 à 0,1764 ou 17,64%.