Distribuição de Poisson
A distribuição de Poisson é uma distribuição descontínua de probabilidade envolvendo dados que podem ser contados, como o número de ocorrências por unidade num intervalo de tempo, de área ou de distância.
É utilizada no cálculo da probabilidade do número de ocorrências de um determinado evento, em um intervalo contínuo de tempo ou espaço. São exemplos de distribuição de Poisson eventos como o número de chamadas telefônicas recebidas em uma delegacia num determinado tempo, quantidade de defeitos por metro em fios produzidos, entre outros.
Na distribuição de Poisson, a unidade de medida (tempo ou espaço) é contínua, mas a variável aleatória (número de ocorrências) é discreta. Portanto, não podemos efetuar a contagem da não ocorrência, ou seja, não podemos estimar o número de ligações telefônicas que deixaram de ser feitas para a delegacia em um determinado tempo.
Os possíveis valores que a variável aleatória x pode assumir na distribuição de Poisson são 1, 1, 2, 3...., sem limite superior.
Características da Distribuição de Poisson
- As ocorrências são independentes e aleatórias;
- A variável aleatória x é o número de ocorrências de um determinado evento ao longo de um intervalo de tempo ou espaço;
A função de probabilidade da variável x será dada pela relação:
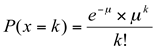
Onde:
µ=λ.t
λ = coeficiente de proporcionalidade
t= tempo ou espaço
Exercício resolvido
O número de pedidos por telefone recebidos em uma pizzaria aos sábados a noite ocorrem a uma taxa de 8 pedidos por hora. Calcule:
a) quantos pedidos são esperados num período de quinze minutos;
x= número de pedidos
λ= 8 pedidos / 1 hora
t= 15 minutos
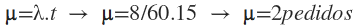
Logo, são esperados 2 pedidos num período de quinze minutos.
b) qual a probabilidade de nenhum pedido ser solicitado em um intervalo de quinze minutos;
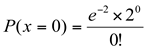
P(x=0) = 0,1353
Logo, a probabilidade da pizzaria não receber nenhum pedido em um período de quinze minutos é 0,1353 ou 13, 53%.
c) qual a probabilidade de ocorrer pelo menos dois pedidos no período de quinze minutos;
Pelo menos dois pedidos é o mesmo que no mínimo dois pedidos, ou seja, dois, três ou n pedidos:
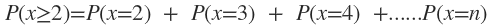
Como a distribuição de Poisson não possui limite superior, será impossível calcular por essa maneira. Assim, o cálculo pode ser pelo complementar, ou seja:
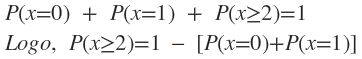
P(x=0)= 0,1353 (já calculado no item b.
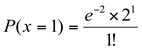
P(x=1) = 0,2706
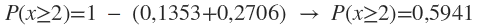
A probabilidade da pizzaria receber ao menos dois pedidos num período de quinze minutos é de 0,5941 ou 59,41%.
d) qual a probabilidade de ocorrer exatamente dois pedidos em vinte minutos.
Será necessário recalcular a média, pois o período mudou de 15 minutos para 20 minutos.
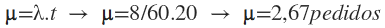
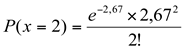
A probabilidade da pizzaria receber exatamente dois pedidos em um período de vinte minutos é de 24,68%.