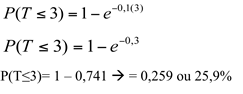Distribuição exponencial
A distribuição exponencial envolve probabilidades ao longo do tempo ou da distância entre ocorrências num intervalo contínuo. Assim, a função de distribuição de probabilidade exponencial é usada como modelo do tempo entre falhas de equipamento elétrico, tempo entre a chegada de clientes em um supermercado, entre outras (STEVENSON, 2001).
A relação entre a distribuição exponencial e a de Poisson é que, enquanto na distribuição de Poisson podemos calcular o numero de ocorrências em um determinado tempo ou espaço, na distribuição exponencial estimamos o tempo ou espaço entre uma ocorrência e outra. Assim, na distribuição de Poisson estimamos a ocorrência da variável aleatória discreta e na distribuição exponencial a variável aleatória contínua.
Se um processo com distribuição de Poisson tem média de λ ocorrências durante um intervalo (de tempo ou espaço), então o espaço entre as ocorrências naquele intervalo será de 1/λ. Exemplificando, se as chamadas telefônicas ocorrem em média à razão de 6 por hora, então o tempo médio entre as chamadas será de 10 minutos.
As probabilidades exponenciais são expressas em termos de tempo ou distância entre ocorrências.
Para calcular a probabilidade de que o tempo ou espaço antes da primeira ocorrência seja maior que um determinado tempo ou espaço empregamos a seguinte fórmula:
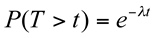
Para calcular a probabilidade de que uma ocorrência ocorra em um intervalo igual a t ou antes de t, usamos:
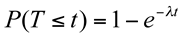
Exercício resolvido
Sabendo que o tempo médio de atendimento do pedido em uma pizzaria seja de 10 minutos e que esse tempo tenha distribuição exponencial, calcule:
a) a probabilidade de um cliente esperar mais do que 10 minutos;
λ = 1 / 10 à λ = 0,1 por minuto
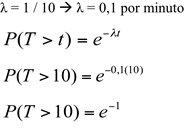
P(T>10) = 0,368 ou 36,8%
b) a probabilidade de o pedido ser atendido em menos de 10 minutos;
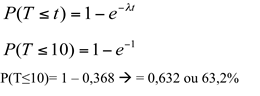
c) a probabilidade de o pedido ser atendido em no máximo 3 minutos.