Distribuições Amostrais
Introdução
Para atingirmos o objetivo de entender o que seja uma distribuição amostral, e a sua utilidade na inferência estatística, vamos primeiramente estabelecer algumas definições e conceituações. Consideremos que tenham sido coletadas várias amostras de uma determinada população, através de um processo estatístico de amostragem. Assim, sabemos que:
- Parâmetro: é toda medida única, descritiva e numérica de uma população;
- Estatística: é o valor obtido através de cálculo, a partir de observações de uma amostra;
- Os valores obtidos de diversas médias amostrais, obtidas a partir de uma população, não são necessariamente iguais entre si, e não são necessariamente iguais ao valor da média da população;
- O conjunto das médias amostrais forma uma série de médias sobre a qual podemos calcular uma média e um desvio padrão;
- A variabilidade nos valores das diversas médias amostrais dá origem a uma distribuição de freqüências, que terá uma média das médias e um desvio padrão da variação das médias em torno da média (das médias);
- Distribuição amostral é a distribuição de frequências das médias amostrais;
- Cada média amostral, denominada estatística, é uma variável aleatória representada por
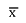 ;
; - Erro padrão é o desvio padrão da distribuição amostral, sendo representado por σ
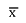 .
. - A média da população representada por μ é um parâmetro, enquanto o parâmetro desvio padrão da população é representado por σ.
Na inferência estatística os parâmetros da população μ e σ serão considerados conhecidos. Na verdade estes parâmetros não são conhecidos, mas essa premissa é útil para o entendimento do conceito de distribuição amostral.
Exemplo 1:
Consideremos 10 grupos de entrevistadores os quais têm como tarefa calcular a média de renda familiar mensal de 50 famílias que vivem em um determinado bairro da cidade. Como todos os grupos levantam dados no mesmo bairro, ao concluírem a tarefa, estes entrevistadores terão formado uma série de 10 médias amostrais representadas como 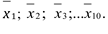
Estas 10 médias amostrais calculadas pelos entrevistadores são denominadas de estatísticas e:
- É de se esperar que os 10 valores das médias amostrais sejam, em sua maioria, diferentes;
- Os valores das médias amostrais poderão ser diferentes do valor da média da população;
- Para as 10 médias amostrais podemos formar uma série e calcular sua média e seu desvio padrão.
Devido ao fato de o valor da média amostral ser uma variável, podemos obter uma distribuição amostral das médias, logo, os valores das médias amostrais têm sua própria distribuição de frequências.
Se outros 10 grupos de entrevistadores fizerem novas amostragens neste mesmo bairro em domicílios selecionados ao acaso, teremos novos valores de médias amostrais, em geral diferentes dos valores obtidos pelos 10 grupos anteriores.
Cada média amostral é uma estatística, sendo também uma variável aleatória que possui uma distribuição de frequências, com um valor próprio de média e de desvio padrão.