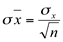Teorema do Limite Central
À medida que o tamanho da amostra aumenta, a distribuição de frequências das médias amostrais tende a se aproximar cada vez mais da distribuição normal.
Se o tamanho n da amostra for suficientemente grande, a média de uma amostra aleatória retirada de uma população de dados, terá uma distribuição de frequências aproximadamente normal independentemente da população. Na prática, uma amostra é considerada suficientemente grande, se consistir de 30 ou mais observações (STEVENSON, 2001).
Já se a população tem distribuição normal, então a média amostral terá distribuição normal qualquer que seja o tamanho da amostra (Figura 1).
Pelo teorema do limite central pode-se afirmar então que a distribuição da média amostral é aproximadamente normal e que os valores da média e desvio padrão estão relacionados com os valores da média e desvio padrão da população, com a única restrição de que a amostra seja grande.
Em sentido estrito, o Teorema do Limite Central só se aplica a médias amostrais (STEVENSON, 2001).
Assim, se uma população de dados tem média μ e desvio padrão σ, da qual se retira uma amostra de tamanho n e média amostral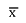 
, pode-se afirmar que:
O valor esperado das médias amostrais E [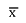] é igual à média da população:
E[ |
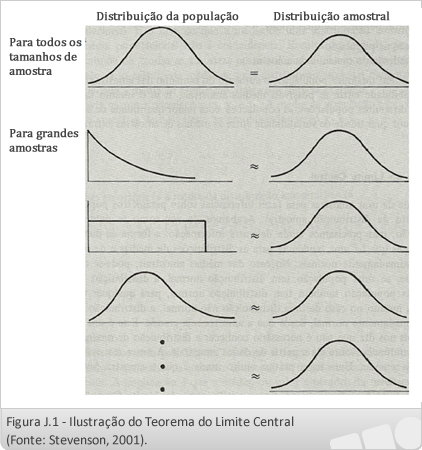
O desvio padrão da distribuição amostral (denominado erro padrão) é igual:
|
Onde:
σ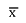 = desvio padrão da distribuição amostral
σx = desvio padrão da população
n = tamanho da amostra
Exemplo 2:
Consideremos uma população formada por 5 empresas aéreas que operam em um aeroporto de uma cidade, e que apresentam os seguintes números de vôos diários:
Empresa |
A |
B |
C |
D |
E |
N° de vôos |
2 |
4 |
6 |
8 |
10 |
Se pretendermos selecionar aleatoriamente uma amostra formada por duas empresas para avaliar o número médio de vôos da cidade, vamos ter um universo de 10 prováveis combinações.
Cada uma das empresas terá a mesma probabilidade de ser selecionada, e dependendo das empresas amostradas o número de vôos médio amostral pode ficar acima ou abaixo da média de vôos da população. Vamos então definir o espaço amostral e determinar o valor esperado das médias amostrais 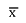de tamanho n = 2 retiradas da população:
Solução:
- A média de vôos da população formada pelas 5 empresas é igual a 6 vôos diários;
- Cada uma das 5 empresas aéreas tem probabilidade igual a 20% de ser sorteada.
- Espaço amostral:
Amostra |
A-B |
A-C |
A-D |
A-E |
B-C |
B-D |
B-E |
C-D |
C-E |
D-E |
Média |
3 |
4 |
5 |
6 |
5 |
6 |
7 |
7 |
8 |
9 |
- Distribuição de Frequências das médias amostrais
Média |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Frequência (%) |
10 |
10 |
20 |
20 |
20 |
10 |
10 |
- Valor Esperado das Médias Amostrais
E[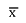] = 3 x 0,1 + 4 x 0,1 + 5 x 0,2 + 6 x 0,2 + 7 x 0,2 + 8 x 0,1 + 9 x 0,1 = 6 = μ
- Distribuição amostral
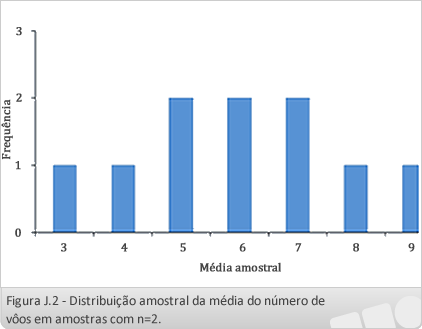
As distribuições amostrais tendem a produzir estatísticas amostrais representativas dos parâmetros populacionais. Apesar do fato de tenderem a apresentar certa variabilidade, podemos dizer que as estatísticas amostrais devem aproximar parâmetros populacionais de forma bastante satisfatória. Assim, esta característica de ser representativa resulta em estatísticas amostrais que tendem a se acumular na vizinhança dos verdadeiros parâmetros populacionais (STEVENSON, 2001). Podemos ver que a Figura 1 apresenta a distribuição amostral da média (amostral), a qual apresenta distribuição normal e com os valores distribuídos ao redor da média amostral (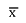= 6,0) que coincide com o valor da média populacional (μ = 6,0).
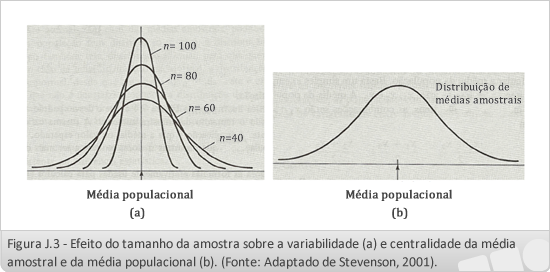
Efeito do tamanho da amostra sobre a distribuição amostral
Na medida em que o tamanho da amostra aumenta, a distribuição amostral tende para a normalidade e a variabilidade amostral decresce, ou seja, em amostragens maiores as médias amostrais tendem a agrupar-se em torno da média populacional, o que é desejável quando se quer estimar a média da população a partir da média amostral, e a variabilidade é menor quando o tamanho da amostra é grande. A Figura 2 mostra esse efeito graficamente.
