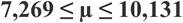Estimativa da média de uma população
Para estimar a média de uma população a partir da média amostral precisamos antes saber se o desvio padrão populacional é conhecido ou não. O método usado é distinto para cada um dos casos e, portanto, iremos abordar primeiramente a estimativa da média quando o desvio padrão da população é conhecido.
Estimativa da média populacional com desvio padrão conhecido
Conforme vimos na aula anterior, quando o desvio padrão populacional é conhecido, as estimativas pontual e intervalar da média populacional são dados por:

Onde σ é o desvio padrão populacional conhecido.
A estimativa intervalar da média populacional assume a hipótese que a distribuição amostral das médias amostrais é normal.
Conforme visto na aula 10, pela aplicação do Teorema do Limite Central, em grandes amostras a hipótese da normalidade não precisa ser testada, entretanto, para amostras de 30 ou menos observações, é importante testar se a população amostrada tem distribuição normal, ou ao menos aproximadamente normal.
De outra forma essas técnicas não podem ser utilizadas (STEVENSON, 2001).
Exemplo 1:
Uma indústria de tubos de aço possui um processo de produção que opera de maneira contínua, através de um turno completo de produção. É projetado para que cada tubo tenha um comprimento de 11m, e o desvio padrão conhecido é de 0,02 m. A intervalos periódicos são selecionadas amostras para determinar se o comprimento médio do tubo ainda se mantém igual a 11m ou se algo de errado ocorreu no processo de produção para que tenha sido modificado o comprimento do tubo produzido. Se tal situação tiver ocorrido, deve-se adotar uma ação corretiva. Uma amostra aleatória de 100 tubos foi selecionada e verificou-se que o comprimento médio do tubo foi de 10,998 m. Estime o comprimento médio de todos os tubos deste processo de produção usando um intervalo de confiança de: a) 95 % e b) 99 %.
a) 95 %
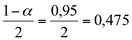
Na tabela da distribuição normal padronizada, para o valor de 0,4750 → z = 1,96
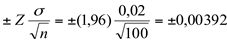
10,998 + 0,00392 = 11,002
10,998 – 0,00392 = 10,994
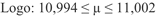
b) 99%
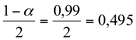
Na tabela da distribuição normal padronizada, para o valor de 0,495 à z = 2,58
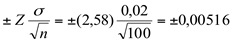
10,998 + 0,00516 = 11,003
10,998 – 0,00516 = 10,993
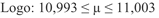
 |  | |
|
A estimativa pontual da média µ = | ||
 |  |
Estimativa da média populacional quando o desvio padrão é desconhecido
Quando o desvio padrão populacional é desconhecido (o que geralmente ocorre), usamos o desvio padrão amostral como estimativa, substituindo σx por Sx nas equações para intervalos de confiança e de erros. Quando o tamanho da amostra é superior a 30 (n>30) o desvio padrão amostral fornece uma aproximação bastante razoável do verdadeiro valor, na maioria dos casos. Entretanto, para amostras de 30 ou menos observações, a aproximação normal não é adequada e devemos usar a distribuição t de Student, que é a distribuição correta quando utilizamos Sx (STEVENSON, 2001).
 |  | |
|
A distribuição t de Student foi criada por W. S. Gossett, funcionário de uma cervejaria irlandesa no princípio do século XX. Como a empresa não permitia que seus funcionários publicassem trabalhos em seu próprio nome, Gossett adotou o pseudônimo de Student em seus trabalhos sobre a distribuição t. Por isso é que ela ficou conhecida como distribuição t de Student (Fonte: Stevenson, 2001). | ||
 |  |
A distribuição t tem sua forma bastante semelhante com a distribuição normal. A principal diferença entre as duas distribuições é que a distribuição t tem maior área nas caudas, o que acarreta um maior valor de t em relação ao correspondente valor z, para um dado nível de confiança.
A distribuição t, diferentemente da normal, não é padronizada e por isso há uma distribuição t (curva) ligeiramente diferente para cada amostra, conforme varia o número de observação (n).
Para amostras de pequeno tamanho (n ≤ 30), a distribuição t é mais sensível ao tamanho da amostra, e para amostras maiores essa sensitividade diminui.
Para grandes amostras é razoável usar valores de z para aproximar valores t, muito embora a distribuição t seja sempre teoricamente correta quando não se conhece o desvio padrão da população, independente do tamanho da amostra (STEVENSON, 2001).
Para consultar uma tabela t precisamos conhecer o nível de confiança desejado e o número de graus de liberdade.
O número de graus de liberdade está relacionado com a maneira como calculamos o desvio padrão amostral:
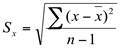
Onde: Sx = desvio padrão amostral
x = valor da variável (de cada amostra)
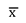 = média amostral
= média amostral
n-1 = graus de liberdade
Logo, o número de graus de liberdade é igual a n-1, ou seja, o tamanho da amostra menos um.
Para facilitar o entendimento de graus de liberdade utilizaremos um exemplo apresentado em Stevenson (2001):
 |  | |
|
Suponhamos que queiramos três números cuja soma seja 10. O primeiro número pode ser tudo (mesmo negativo); o segundo número também. Mas o terceiro número está limitado à condição que a soma dos três deve ser 10. Escolhidos os dois primeiros valores, o terceiro está essencialmente determinado, não existe grau de liberdade para o terceiro valor. Há três números em jogo, mas liberdade só para dois. | ||
 |  |
O que é exigido é que a soma dos desvios em relação à média amostral seja zero, o que obriga um arredondamento do menor valor. Logo, o número de graus de liberdade é igual a n-1.
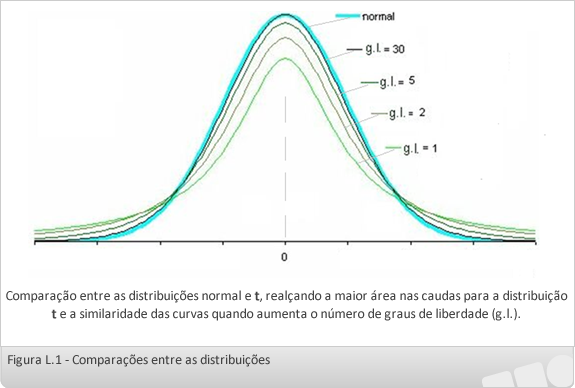
A Figura 1 apresenta a curva normal padronizada e a curva da distribuição t de Student, onde pode ser observada a maior área sobre as caudas para a distribuição t e a aproximação entre as duas curvas quando o número de graus de liberdade cresce (n=31, g.l.=30).
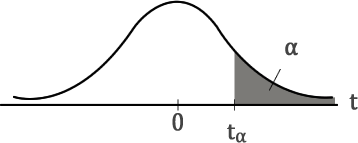
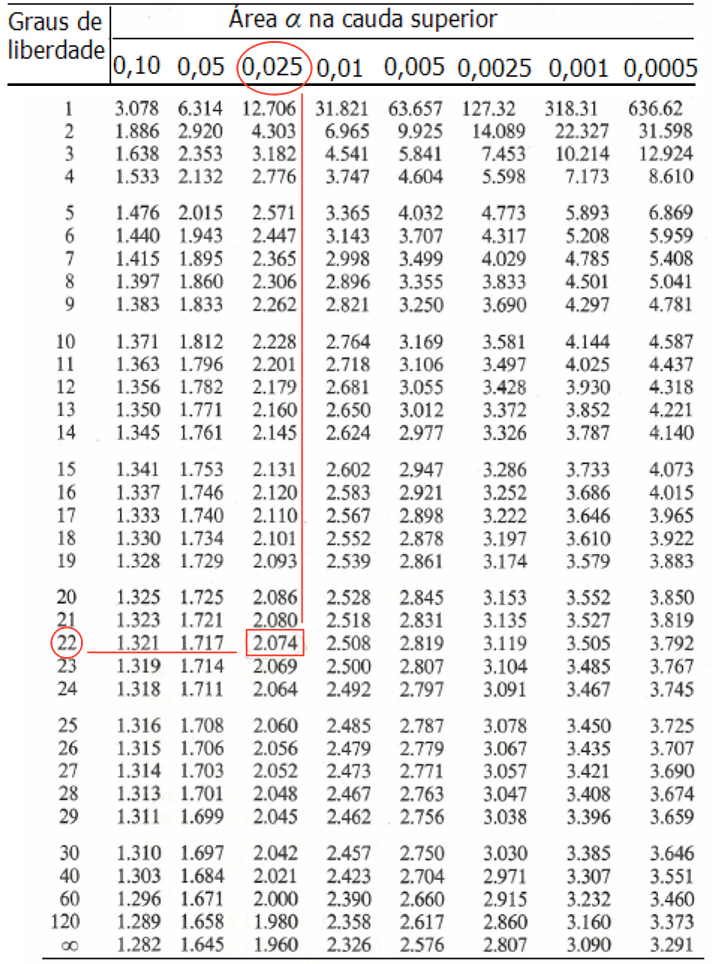
A Tabela 1 apresenta os valores t da distribuição de Student. Para utilizar a tabela precisamos conhecer, como escrito anteriormente, o nível de confiança desejado (que está representado na Tabela 1 pela área abaixo da curva para tα), na primeira linha, e o número de graus de liberdade (n-1), que aparece na primeira coluna da tabela. O exemplo a seguir mostra como utilizar a tabela t.
Exemplo 2:
Queremos saber o valor de t para uma amostra de n=23, para um intervalo de confiança de 95%.
95% = 0,95 à 0,05 (nas duas caudas) = 0,05 ∕ 2 = 0,025 (área na cauda superior)
n= 23 à número de graus de liberdade = n-1 à g.l.=22
Entrando na Tabela 1 com os valores de g.l.=22 e α = 0,025, encontramos o valor de 2,074 para t.
Convém salientar que a distribuição t só é teoricamente adequada quando a distribuição é normal. Na prática, quando n é maior do que 30 observações, a necessidade de admitir a normalidade diminui (STEVENSON, 2001).
Exemplo 3:
A seguinte amostra foi extraída de uma população com distribuição normal:
[ 9 – 8 – 12 – 7 – 9 – 6 – 11 – 6 – 10 – 9 ]
Estime o valor da média populacional com um intervalo de confiança de 95%.
Solução:
Média da amostra: 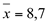
Desvio padrão amostral: 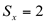
Como 1-α = 0,95 teremos: α = 1- 0,95 → 0,05 (nas duas caudas), logo, na Tabela 1 (unicaudal) teremos:
α = 0,05 / 2 → α = 0,025
Graus de Liberdade: n-1 → 10 – 1 , logo g.l. = 9
Consultando a Tabela t obtemos o valor de tα = 2,262
Para o intervalo de confiança bicaudal temos: tα = ±2,262
Substituindo na fórmula 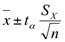
teremos:
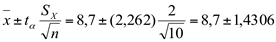
Resposta: |