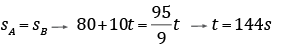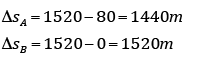Velocidade e Aceleração Instantânea e Média
Velocidade
Velocidades- v
![]()
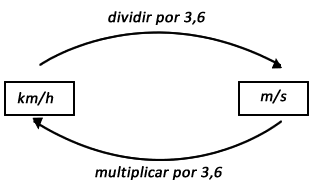
Unidade: metros / segundo
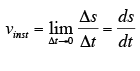
Aceleração média
A aceleração é relacionada com uma variação da velocidade.
Para definirmos a aceleração escalar média, vamos considerar um móvel percorrendo a trajetória da figura.
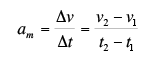
Se a velocidade for constante, isto é, for sempre a mesma, o movimento é dito uniforme, se a velocidade variar, isto é, não for sempre a mesma, o movimento é dito variado.
Num certo intervalo de tempo de um movimento variado pode ocorrer aumento ou diminuição da velocidade, com maior ou menor rapidez.
A aceleração escalar média mede a rapidez dessa variação da velocidade.
A aceleração escalar média é numericamente igual à variação de velocidade na unidade de tempo.
As unidades mais comuns de aceleração são: m/s², cm/s² e Km/h².
Aceleração instantânea
Aceleração escalar é o limite para o qual tende a aceleração escalar média quando o ∆t tende a zero.
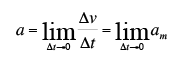
1) Movimento acelerado: um movimento é denominado acelerado quando o módulo da velocidade aumenta no decorrer do tempo.
Isso ocorre quando a velocidade e a aceleração têm o mesmo sinal.
![]()
2) Movimento retardado: quando o módulo da velocidade diminui no decorrer do tempo, o movimento é dito retardado.
Isso ocorre quando a velocidade e a aceleração têm sinais contrários.
![]()
Movimento Uniforme (a = 0)
Considerando um carrinho transportando um vasilhame com certa quantidade de líquido, em que está instalada uma torneira que pinga gotas desse líquido a intervalos de tempo iguais.
As distâncias entre as marcas deixadas sobre um papel pelas gotas do líquido durante o movimento do carrinho são iguais.
Isso mostra que o carrinho percorre distâncias iguais em intervalos de tempo iguais, então dizemos que eles realizam um movimento chamado movimento uniforme (MU).
O movimento da Terra em torno do seu eixo, o movimento dos ponteiros de um relógio e a viagem de uma nave interplanetária são exemplos bem próximos do movimento uniforme.
Na prática, os movimentos não são perfeitamente uniformes.
Se a trajetória for retilínea, o movimento é dito movimento retilíneo e uniforme (MRU).
Funções Horárias
Conhecidas as características do movimento, vamos agora estabelecer as leis que regem o movimento uniforme. Se a forma da trajetória for conhecida, essas leis permitem determinar, em cada instante, a posição, a velocidade e a aceleração de um corpo em movimento.
Posição em função do tempo [s = f(t)]
S0 = posição do móvel no instante t0 = 0.
S= a posição do móvel no instante t.
Velocidade em função do tempo [v = f (t)]
v = f (t) = constante ≠ 0
Isso significa que o móvel tem, em toda a trajetória, a velocidade do início do movimento.
Aceleração em função do tempo [a = f(t)]
a f(t) = 0
Isso quer dizer que não existe variação de velocidade durante o movimento.
Gráficos
Posição em função do tempo [s=f(t)]
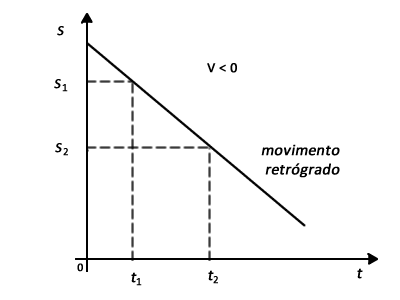
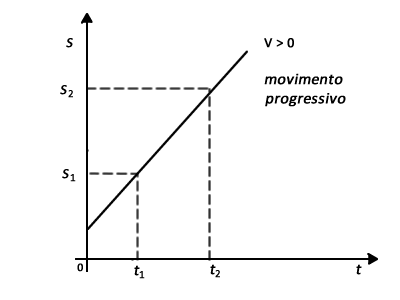
Observações
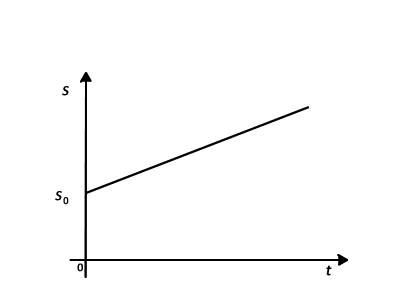
1) O valor da ordenada em que a reta corta o eixo s representa o valor de s0.
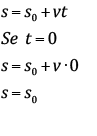
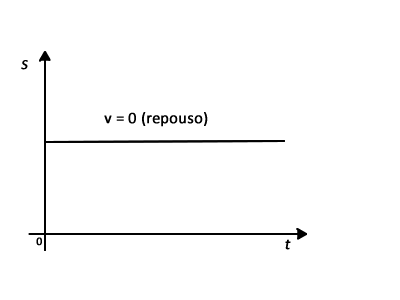
2) Quando o corpo não estiver em movimento, isto é, v = O, a posição do móvel é sempre a mesma.
3) No gráfico s = f (t), a tgα é numericamente igual à velocidade.
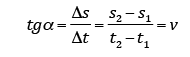
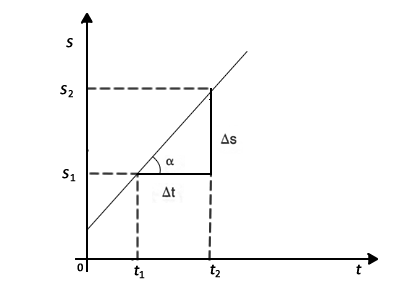
Quanto maior for a velocidade do corpo, mais inclinada em relação ao eixo dos tempos é a reta que representa o movimento.
Velocidade em função do tempo [v= f (t)]
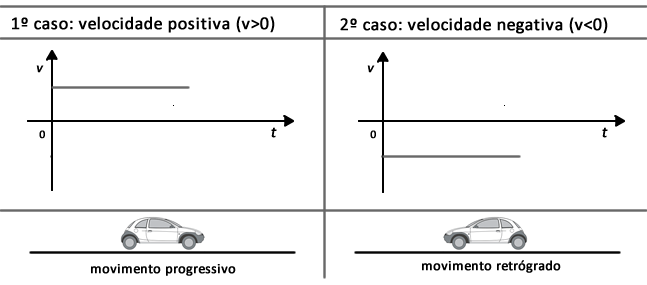
Aceleração em função do tempo [a= f(t)]
Exercício B 1:
Um ciclista A está com velocidade constante VA = 36 km/h, um outro ciclista B o persegue com velocidade constante 38 km/h. Num certo instante, a distância que os separa é de 80 m.
a) A partir desse instante, quanto tempo o ciclista B levará para alcançar o ciclista A?
b) Determine a posição dos ciclistas quando se encontraram.
c) Calcule a distância percorrida pelos dois ciclistas.
a) Para se obter o tempo igualamos as posições dos ciclistas A e B.
b) Para achar a posição do encontro devemos substituir t = 144 s em qualquer uma das funções horárias, pois, nesse instante, as posições dos ciclistas são iguais.
c)
Respostas: a) 144 s; b) 1520 m; c) = 1 440 m; SB = 1 520 m