Movimento Circular Uniforme
Um ponto material está animado de um movimento circular uniforme (MCU) quando sua trajetória é uma circunferência e o módulo de sua velocidade permanece constante no decorrer do tempo.
![]()
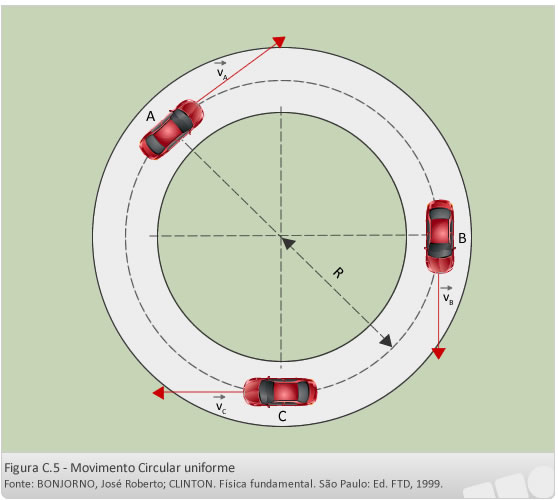
No dia a dia, vemos muitos exemplos: um disco, as pás de um ventilador, um carrossel, um satélite em volta da Terra.
Frequência
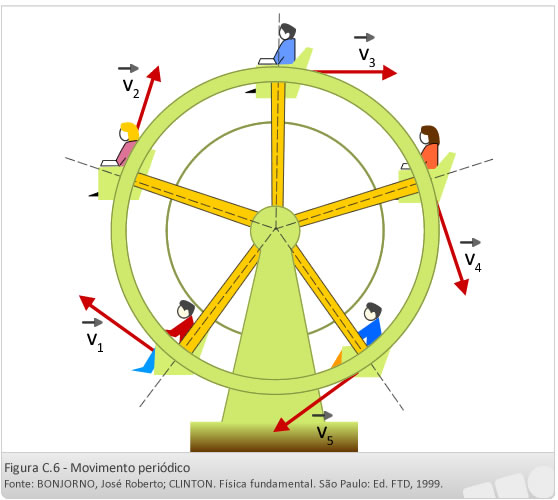
Durante esse movimento, cada cadeira da roda-gigante descreve circunferências, continuamente. Ou seja, cada uma delas passa repetidas vezes pela mesma posição e nas mesmas condições de velocidade e aceleração, em intervalos de tempo iguais. Devido a isso, o movimento de rotação da roda-gigante é considerado periódico.
O número de voltas (ou ciclos) que a roda-gigante efetua na unidade de tempo é chamado sequência do movimento.
Se, por exemplo, cada cadeira dá 15 voltas por minuto, dizemos que a roda-gigante gira com uma frequência de 15 ciclos por minuto ou 15 rotações por minuto (15 rpm).
Se quisermos achar a frequência em segundos, basta dividirmos por 60.
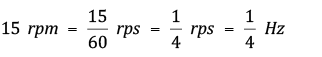
A unidade ciclos por segundo ou rotações por segundo é chamada hertz (Hz).
Por outro lado, o tempo que a roda-gigante leva para dar uma volta completa é denominado período do movimento.
Podemos achar o período do movimento da roda-gigante estabelecendo uma regra de três simples: se a roda-gigante dá de volta por segundo, então, o tempo gasto para dar uma volta completa é T. O período é o inverso da frequência.
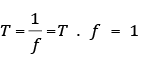
Exercício 3 C:
Qual é o período e a freqüência de cada um dos três ponteiros de um relógio?
Velocidade Linear, Velocidade escalar ou Velocidade tangencial
É o arco de circunferência descrito no intervalo de tempo.
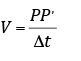
PP’ → arco de circunferência ( em metros)
Δt → intervalo de tempo( em segundos)
V → velocidade linear (em m/s)
A velocidade linear pode ser fornecida pelas seguintes relações:

R → arco de circunferência (em metros)
T
→ intervalo de tempo(em segundos)
f
→ velocidade linear (em m/s)
Velocidade Angular Média
Considere um móvel percorrendo uma trajetória circular de raio R e os ângulos φ1 e φ2 quando o móvel se encontra nos instantes t1 e t2 respectivamente. Define-se como velocidade angular média o quociente entre o ângulo descrito, ∆φ, e o tempo, ∆t, gasto para descrevê-lo.
![]()
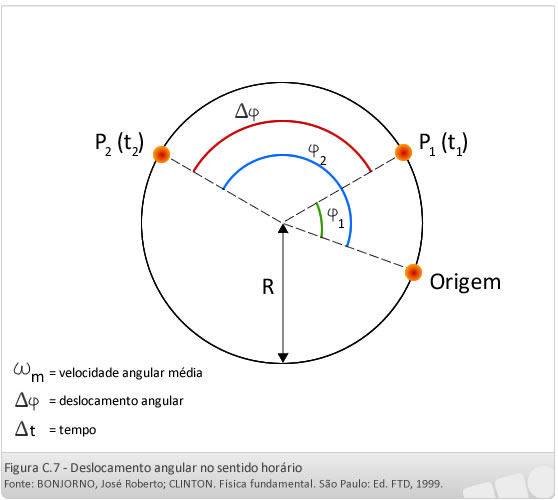
No SI, os ângulos são medidos em radianos. Assim, a unidade de velocidade angular é rad/s.
Relação entre velocidade Linear e angular:

R → arco de circunferência ( em metros)
V
→ intervalo de tempo( em segundos)
w
→ velocidade linear (em m/s)
Exercício 4 C:
Consideremos um corpo movimentando-se n trajetória circular de raio 5m. No instante t1 = 2s sua posição é definida pelo ângulo de fase φ1 = 30º e no instante t2 =8s sua posição é definida pelo ângulo de fase φ2= 90°.
Determine:
a) o deslocamento angular nesse intervalo de tempo
b) a velocidade angular média, em rad/s.
c) a velocidade escalar média, em m/s.
Aceleração Centrípeta
Embora o valor numérico da velocidade linear de um ponto material seja sempre o mesmo, ela não é constante, porque sua direção e sentido variam de ponto para ponto.
Se a velocidade varia, é porque existe uma aceleração agindo sobre esse ponto material, essa aceleração denomina-se aceleração centrípeta.
A aceleração centrípeta é sempre dirigida para o centro da circunferência descrita pelo ponto material e é responsável somente pela variação da direção da velocidade. Ela não altera o módulo da velocidade.
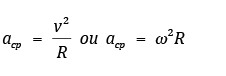
Exercício 5 C:
Um ponto material descreve uma trajetória circular de raio igual a 20m, com velocidade escalar constante igual a 4π m/s. Utilizar π²= 10.
Determine:
a) velocidade angular da partícula, em rad/s.
b) o módulo da aceleração centrípeta em m/s2
c) o número de voltas efetuadas pelo ponto material a cada segundo
Função Angular Horária
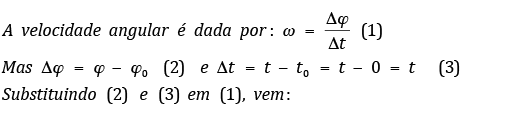
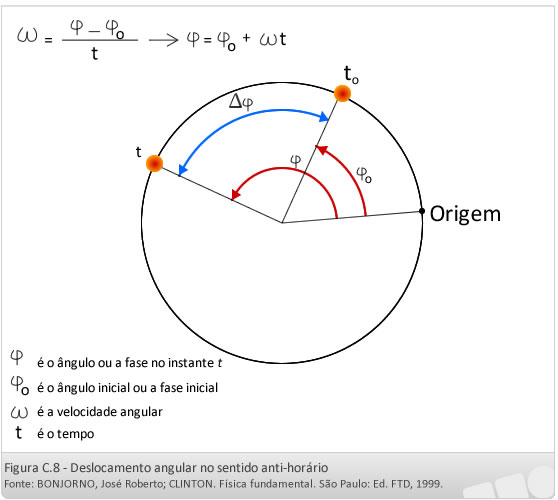
Exercício 6 C:
Um móvel percorre uma circunferência de 3m de raio, efetuando meia-volta por segundo. Sabendo-se que no início da contagem dos tempos ele se encontra na origem dos arcos, calcule:
a) a freqüência, em Hz.
b) o período, em s.
c) a velocidade angular, em rad/s.
d) a velocidade escalar, em m/s.
e) as funções horárias do movimento sob as formas linear e angular.
f) a aceleração centrípeta em m/s2.
Polias
Seja a polia A, de raio RA, fixa no eixo de um motor que gira com uma frequência. Ela está acoplada, por meio de uma correia, a outra polia de raio RB. Qual a frequência de rotação B da polia B?
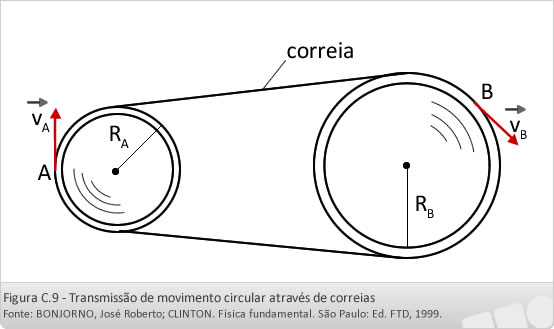
Admitindo-se que a correia seja inextensível, todos os seus pontos possuem a mesma velocidade escalar.
Admitindo-se que não haja escorregamento, os pontos periféricos de cada polia possuem a mesma velocidade escalar, que é igual à velocidade escalar da correia, isto é:
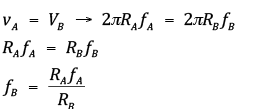
Se RB for maior que RA haverá uma diminuição de frequência; se RB for menor que RA haverá um aumento de frequência.
No caso abaixo, A e B descrevem o mesmo ângulo central φ e mesmo intervalo de tempo.
Duas opções:
A velocidade angular de um ponto periférico da polia A é igual à velocidade angular de um ponto periférico da polia B, ωA = ωB.
O período e a frequência das polias A e B são iguais.
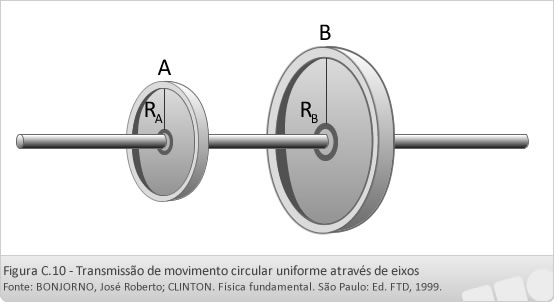
Exercício 7 C:
Duas polias, A e B, de raios RA = 30cm e RB = 5cm giram acopladas por meio de uma correia. A polia A efetua 10 rpm. Determine o número de rotações da polia B.

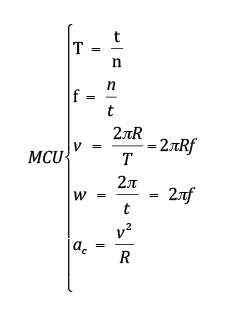
Legenda:
R → raio ( em metros)
T → período (em segundos)
f → freqüência (em hz)
R → raio ( em metros)
V → velocidade linear (em m/s)
w → velocidade angular (em rad/s)
ac → aceleração centrípeta (em m/s2)
t → tempo (em segundos)
n → numero de voltas