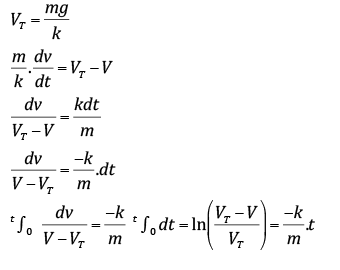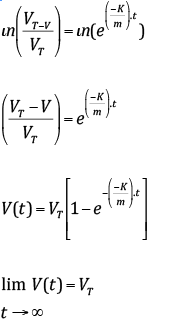Força de atrito - ( ƒ )

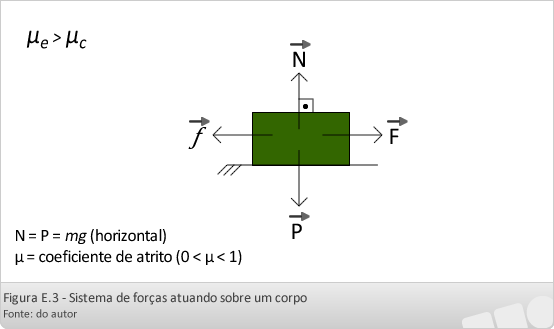
Sendo a força de atrito(f), geralmente em sentido oposto ao movimento e dada pela relação:

Sendo N a força de reação normal, que no plano inclinado é igual ao P_Y.

A força de atrito estático máxima que a força de atrito cinético, ou seja:

µ_e>µ_c

Aceleração de um corpo descendo um plano inclinado com atrito:

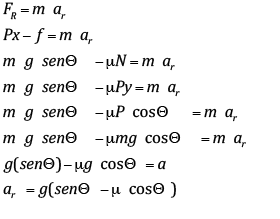
Onde µ → coeficiente de atrito cinético (adimensional).

Exercício E 1:

No sistema abaixo, os corpos A e B possuem massas iguais entre si a 20 kg. O fio e a roldana são ideais. O coeficiente de atrito cinético entre o plano inclinado e o corpo A vale 0.2. Considerando g = 10 m/s², determine:

A aceleração que o sistema adquire, em m/s²
A força de tração que atua no fio, em N.

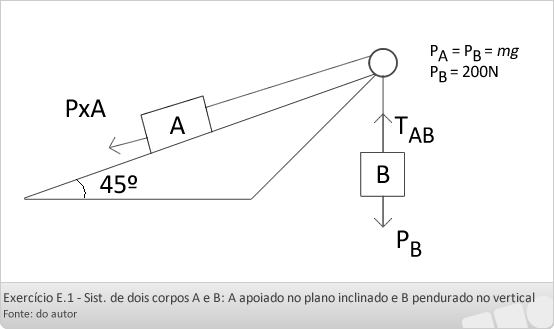
P_yA = P_xA= P sen.45° = 200x0,7 = 140N
N_A = P_YA
ƒ_A =µ N_A = 0,2 x P_yA = 0,2 x140 = 28N

a) F_R = m_ar
(m_A+m_B) a_r
200 – (140 +28) = 40_ar
a_r = 0, 8 m/s²

b) F_RB = m _ar
P_B – T = m_B a_r
200 – T = 20 x 0,8
T = 184N

Exercício E 2:

No sistema abaixo, os corpos A e B possuem massas respectivamente iguais a 20 kg e 40 kg. O fio e a roldana são ideais. Os coeficientes de atrito cinético entre os planos inclinados e os corpos A e B valem respectivamente 0.2 e 0,1. Considerando g = 10 m/s², determine:

A aceleração que o sistema adquire, em m/s²
A força de tração que atua no fio, em N.

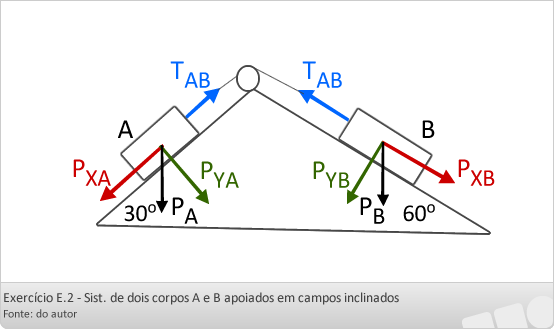
P_xA = P sen30º =200 x 0,5 = 100N
P_yA = P cos30º =200 x 0,9 = 180N
N_A = P_yA = 180N
ƒ_A = µ_AN_A = 0,2 x 180 = 36N

P_xB = P_B sen60º =400 x 0,9 = 360N
P_yB = P_Bcos 60º =400 x 0,5 = 200N
N_B = P_yB = 200N

ƒ_B = µ_{BN_{B = 0,1 x 200 = 20N}}

a) F_R = m _ar
P_xB – (P_xA + ƒ_A + ƒ_B) = (m_A +m_B) _ar
360 – (100 +36+20) = 60 _ar
_ar = 3,4 m/s²

b) F_RB = m _ar
P_xB – ( T+ ƒ_B) = m _ar
360 – T - 20 = 40 x 3,4
T = 204N

Exercício E 3:

No sistema abaixo, um corpo de massa 5 kg se encontra apoiado sobre um plano horizontal. O corpo é puxado por uma força horizontal de 60N e adquire uma aceleração de 4 m/s². Considerando g = 10 m/s², determine o coeficiente de atrito cinético entre o corpo e o plano.

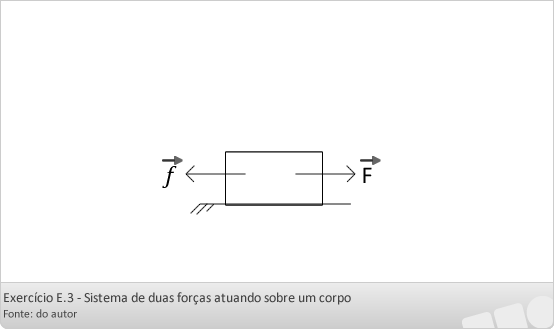
F_R = m _ar
F-f = m _ar
60 – f =m _ar
60- (µ. m. g) = 5 x 4
60-50 µ=20
µ = 0,8

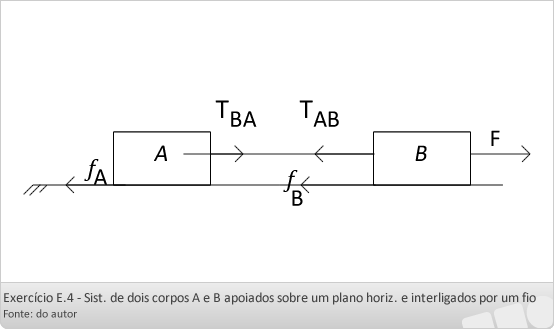
Exercício E 4:

No sistema abaixo, os corpos A e B, de massas respectivamente iguais 5 kg e 3 kg, estão apoiados sobre um plano horizontal e interligados por um fio ideal. O corpo B é puxado por uma força horizontal de 57N. Os coeficientes de atrito cinético entre o plano horizontal e os corpos A e B valem respectivamente 0,2 e 0,5. Considerando g = 10 m/s², determine:

A aceleração que o sistema adquire, em m/s²
A força de tração que atua no fio, em N.

a) FR = m _ar
F – (ƒ_A + ƒ_b) = (m_A + m_B ) _ar
57 – ( 10 + 15) = (5 + 3) _ar
_ar = 4m/s^²

b) F_RA= m_B.a
(T_BA - f_A) = m_A.a
T_BA-10=5 x 4
T_BA = 30

ƒ_A = µ_A N_A = 0,2 x 5 x 10 à ƒ_A = 10N

ƒ_B = µ_B N_B = 0,5 x 3 x 10 à ƒ_B = 15N

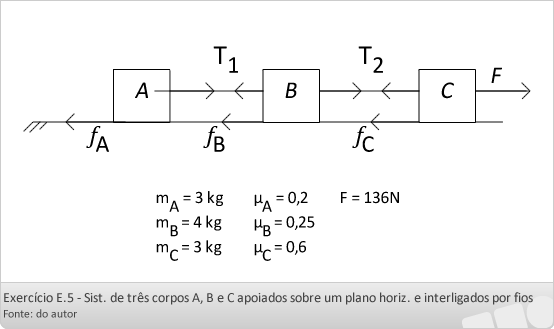
Exercício E 5:

No sistema abaixo, os corpos A, B e C de massas respectivamente iguais 3 kg e 4 kg e 3 kg, estão apoiados sobre um plano horizontal e interligados por um fio ideal. O corpo C é puxado por uma força horizontal de 136N. Os coeficientes de atrito cinético entre o plano horizontal e os corpos A, B e C valem respectivamente 0,2, 0,25 e 0,6. Considerando g = 10 m/s², determine:

a) A aceleração que o sistema adquire, em m/s²
b) A força de tração T1 que atua no fio 1, em N.
c) A força de tração T2 que atua no fio 2, em N.

ƒ_A = µ_A N_A = 0,2 x 3 x 10 à ƒ_A = 6N

ƒ_B = µ_B N_B = 0,25 x 4 x 10 à ƒ_B = 10N

ƒ_C = µ_C N_C = 0,6 x 3 x 10 à ƒ_C = 18N

a) F_R = m _ar
F – (ƒ_A + ƒ_B+ ƒ_C) = (m_A + m_B + m_C ) x a
136 – (6 + 10 + 18) = (3 + 4 +3) x a
a = 10,2 m/s^²

b) F_RA = m _ar
T₁ – A = 3 x 10,2
T₁ – 6 = 36,6N
T₁ = 42,6N

c) F_RC = m _ar
F – (T₂ + C) = 3 x 10,2
136 – (T₁ + 18)=30,6
T₁ = 87,4N

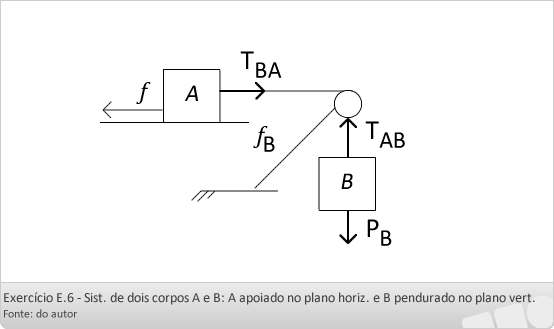
Exercício E 6:

No sistema abaixo, os corpos A e B possuem massas respectivamente iguais 4 kg e 1kg. O fio e a roldana são ideais. O coeficiente de atrito cinético entre o plano horizontal e o corpo A vale 0.4. Considerando g = 10 m/s², determine:

a) A aceleração que o sistema adquire, em m/s²
b) A força de atrito estático f que atua no corpo A, em N.
c) A força de tração que atua no fio, em N.
d) A força de atrito estático máxima que atua no corpo A, em N.

a) aceleração é nula, pois a força de atrito máxima vale 16N, valor superior a força do peso do corpo B, que deveria ser a força máxima do sistema, logo não consegue “puxar” o sistema.
F_R=0 → a=0

b) F_R=0 → f-P_B = 0 → f=P_B à f=m_B.g →f=10N.

c) F_RB=0 → T_AB-_PB = 0 → T_AB=_PB → T_AB = m_B.g → T_AB = 10N.

d) f_A=μ.N_A → f_A=μ.m_A.g → f_A=0,4.4.10 → f_A=16N.

Exercício E 7:

Um objeto está com velocidade 108 km/h horizontal quando penetra numa região rugosa, parando após percorrer 100m. Sendo sua massa igual a 5 kg, determine o coeficiente de atrito cinético µ entre o plano rugoso e o objeto.

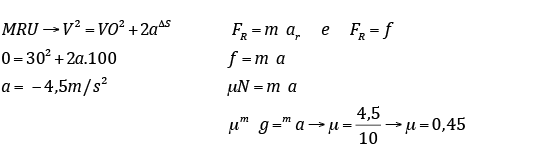
Força de atrito com o ar

Fluido que gera força de arrasto (atrito).

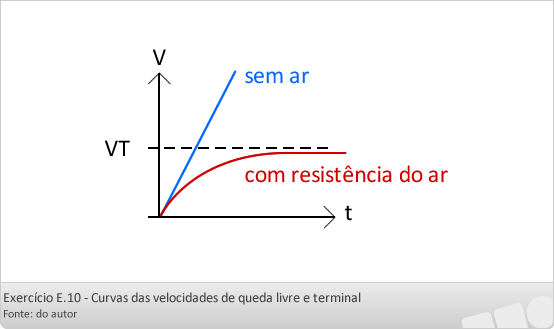
Inicialmente seria MQL, mas se torna MRU, porque a aceleração é zero.

Velocidade terminal (V): Também definida como velocidade limite, é a velocidade no instante em que a força de se resistência do ar se torna igual a força peso do corpo. A partir deste instante o movimento torna-se uniforme.

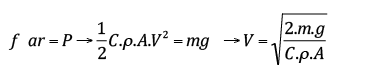
Exercício E 8:

Uma gota de chuva de raio 1,5 mm cai de uma nuvem que esta em uma altura de 1.200m. Considere o coeficiente de arrasto C = 0,6; densidade da água & = 1g/cm³; densidade do ar 1,2 x 10-³g/cm³ e que a gota d’água seja uma esfera perfeita. Determine:

a)Velocidade terminal:

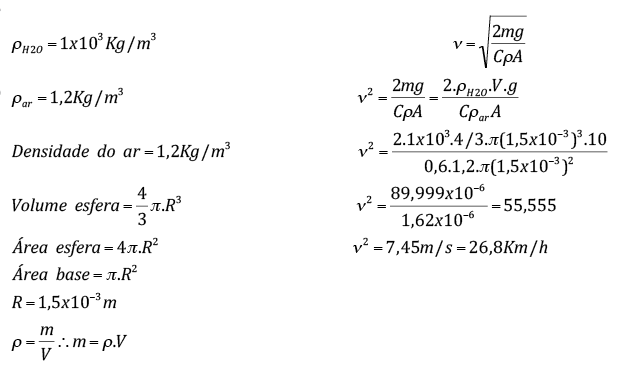
b) velocidade da gota d’água ao tocar o solo em queda livre: V =557,7km/h

MQL → V² = Vo² + 2gh
V² = 0 + 20 x 1200
V= 154,92 m/s → V =557,7 km/h

Exercício E 9:

Um gato jogado do décimo andar atinge velocidade terminal de 97 km/h, caindo horizontalmente encolhido. Se ele caísse todo esticado, de tal maneira que sua área dobrasse, qual seria a nova velocidade terminal?

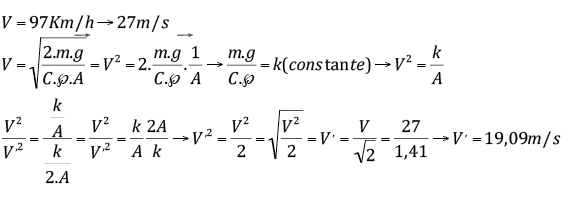
Exercício E 10:

Determinar a velocidade terminal de uma pedra, quando jogada em um lago profundo.

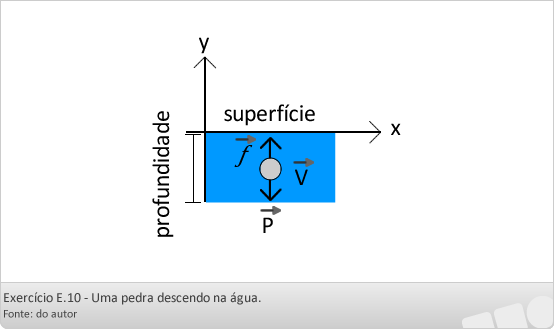
Sendo VT a velocidade terminal

UNIDADE E – Aplicações das Leis de Newton