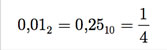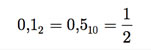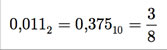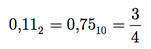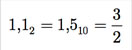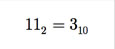B.2 Sistemas de representação de números em um computador digital
Primeiramente, vamos analisar como os números são representados em um computador. Vamos dividir o nosso estudo em duas etapas: (i) para números inteiros; e (ii) para números reais.
Representação de um número inteiro
A representação de um número inteiro, a princípio, não apresenta nenhuma dificuldade. Qualquer computador opera internamente com uma base fixa b, onde b é um inteiro maior ou igual a 2, e é escolhido como uma potência de 2.
Assim, dado um número inteiro n ¹ 0, este possui uma representação única dada por
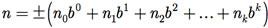
onde os ni, i = 0, 1, 2, ..., k são inteiros que satisfazem 0 ≤ ni ≤ b e nk ≠ 0.
Por exemplo, na base b = 10, o número 54672 é representado por
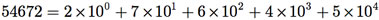
e são armazenados os coeficientes n0 = 2, n1 = 7, n2 = 6, n3 = 4 e n4 = 5.
Representação de um número real
Um computador ou calculadora representa um número real em um sistema denominado sistema de ponto flutuante normalizado. Um número real r é dito um número de ponto flutuante normalizado se atender as seguintes condições:
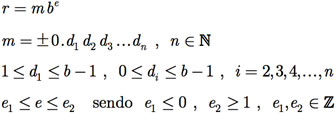
onde b é a base do sistema de ponto flutuante, b ≥ 2;
m é a mantissa do número;
e é o expoente do número, com e1 sendo o menor e e2, o maior;
n é o número máximo de dígitos que podem ser utilizados na representação do número. É conhecido como precisão da máquina;
di são os dígitos da mantissa, com i = 1, 2, 3,..., n.
A união de todos os números de ponto flutuante com o zero, que é representado por
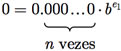
é chamado de Sistema de Ponto Flutuante.
Para facilitar a especificação do sistema de ponto flutuante de uma máquina digital, usualmente, o representamos por F(b, n, e1, e2), onde e1 e e2 são, respectivamente, o menor e o maior expoente, b é a base do sistema de numeração e n é a precisão da máquina.
Para exemplificar este procedimento de representação de um sistema de ponto flutuante, considere a calculadora científica da Hewlett-Packard HP 48G. O seu sistema de ponto flutuante é F(10, 12, -500, 499). Portanto, essa calculadora opera com o sistema numérico decimal, utiliza como precisão 12 dígitos (as mantissas são representadas por 12 dígitos), e o menor e o maior expoente valem, respectivamente -500 e 499.
a) Propriedades dos Números em Sistemas de Ponto Flutuante
Seja um sistema de ponto flutuante especificado por F(b, n, e1, e2).
a.1) O menor número, em valor absoluto, que pode ser representado é
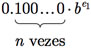
a.2) O maior número, em valor absoluto, que pode ser representado é
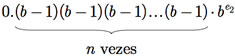
a.3) Quantidade total de números que podem ser representados
Lembre que o primeiro dígito da mantissa deve ser diferente de 0. Assim, para a primeira posição da mantissa, temos (b - 1) dígitos possíveis. Para as (n - 1) posições restantes da mantissa, podemos ter b dígitos. Por outro lado, cada uma dessas mantissas pode ter um dos (e2 - e1 + 1) expoentes possíveis (note que o + 1 é para considerar o expoente zero). Ainda temos que incluir o número 0 e considerar que os números podem ser positivos e negativos. Dessa forma, considerando todas as possibilidades, chegamos a um total de
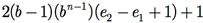
números de ponto flutuante passíveis de serem representados no sistema F(b, n, e1, e2).
a.4) Para qualquer mantissa m, temos que b-3 £ |m| < 1.
|m| < 1, pois toda mantissa deve ter o dígito zero antes do ponto;
|m|3 b-1 , não teríamos o número normalizado, pois o primeiro dígito da mantissa (após o ponto) seria nulo.
Os exemplos a seguir irão ilustrar os aspectos importantes em relação à representação dos números reais em sistemas de ponto flutuante.
Exemplo B.1: Considere o sistema de ponto flutuante hipotético F(10, 2, -1, 1).
O total de números reais que podem ser representados nesse sistema é
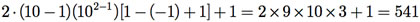
O menor número é 0.10 ´ 10-1 = 0.01 e o maior, 0.99 ´101 = 9.9, em valores absolutos.
Exemplo B.2: Considere agora o sistema de ponto flutuante hipotético F(2, 3, -1, 2).
O total de números reais que podem ser representados nesse sistema é
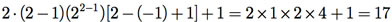
O menor número é 0.10 ´ 2-1 = 0,012 = 0,2510 e o maior, 0.11 ´102 = 112 = 3, em valores absolutos.
A Tabela B.1 mostra todos os números reais que podem ser representados nesse sistema de ponto flutuante. A primeira linha da tabela corresponde a todos os expoentes possíveis, enquanto que a primeira coluna corresponde a todas as mantissas possíveis. A tabela apresenta os 8 números positivos que podem ser representados no sistema de ponto flutuante do exemplo.
|
-1 |
0 |
1 |
2 |
0.10 |
|
|
|
|
0.11 |
|
|
|
|
Todos os números que podem ser representados no sistema de ponto flutuante F (2, 3, -1, 2) estão assinalados na reta dos números reais, conforme mostra a Figura B.1.
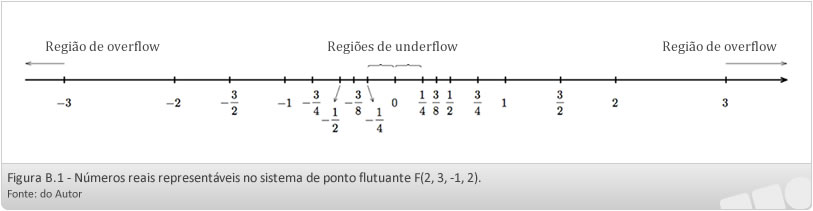
Pela observação da Tabela B.1, percebemos que não se consegue representar números em ponto flutuante menores que 0,25 e nem maiores que -0,25. Essa região é conhecida como região de underflow da máquina. De forma semelhante, números em ponto flutuante maiores que 3 e menores que -3 também não são passíveis de representação. Essa é a região de overflow da máquina. Assim, definimos essas regiões como:
- Região de underflow:
- Corresponde às regiões entre o maior número de ponto flutuante negativo e o zero e entre o zero e o menor número de ponto flutuante positivo. No Exemplo B.2, esta região corresponde a ( - 1/4 , 0 ) ∪ ( 0, 1/4 )
- Região de overflow:
- Corresponde às regiões aquém do menor número de ponto flutuante negativo e além do maior número de ponto flutuante positivo. No Exemplo B.2, essa região corresponde a ( - ∞ , -3) ∪ ( 3,∞ ).
Exemplo B.3: Considere o sistema de ponto flutuante F(10, 2, -1, 2). Neste sistema, os números x = 0,068 e y = 0,039 são representados, respectivamente, por x = 0,68.10-1 e y = 0,39.10-1. Observe que ambos os números possuem representação exata no sistema de ponto flutuante dado.Agora, vamos realizar a soma entre os números x e y. Utilizando o conjunto dos números reais, temos que o resultado da soma é 0,107. Escrevendo o resultado na forma de ponto flutuante normalizado, temos 0,107.100. Observe que este resultado, quando escrito no sistema de ponto flutuante do Exemplo B.3, será armazenado como 0,10.100 ou como 0,11.100, dependendo do sistema de arredondamento que a máquina utilizar. Percebe-se, então, que embora os operandos numéricos possuam representação exata no sistema de ponto flutuante, a sua soma apresentará um resultado errôneo, pois ela não é passível de ser representada exatamente no sistema de ponto flutuante.
Os exemplos apresentados têm por objetivo chamar a atenção de você estudante para possíveis problemas numéricos que podemos encontrar quando trabalhando com máquinas digitais. É muito importante você ter claro em sua mente que:
- Os sistemas de ponto flutuante utilizados pelos computadores digitais não são capazes de representar com exatidão todos os números do conjunto dos números reais;
- Mesmo que os números a serem operados possuam representação exata, é possível que o resultado da operação não o possua.
.png)