B.3 Erros absolutos e erros relativos
Definimos como erro absoluto (EA) a diferença entre o valor exato de uma medida numérica x* e o seu valor aproximado x. Assim, matematicamente, temos
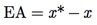
Em geral, somente conhecemos o valor x para a medida e, assim, é impossível obter o valor exato do erro absoluto. Sendo assim, o que se faz é obter um limite superior ou uma estimativa para o módulo do erro absoluto.
Considere, por exemplo, o número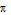 
. Sabemos que 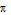* ∈ (3,14; 3,15). Tomando para 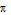qualquer valor dentro do intervalo dado, teremos | EA | = |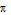* - 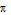| < 0,01.
Por outro lado, o erro absoluto nem sempre descreve com precisão um cálculo. Esse fator está associado à ordem de grandeza dos números envolvidos. Por esse motivo, utilizamos também um outro tipo de erro para essa análise, o erro relativo.
O erro relativo é definido como o erro absoluto dividido pelo valor aproximado. Matematicamente,
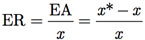
Exemplo B.4: Considere as medidas para os números x = 987,3 com |EAx| < 0,1 e y = 3,2 com |EAy| < 0,1.
Analisemos, primeiramente, o número x. Com o erro relativo |EAx|, temos que o valor exato para x* ∈(987,2; 987,4). O erro relativo para a medida x é, então,
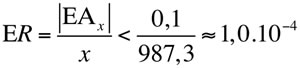
outro lado, para a medida y temos que o seu valor exato é y* ∈(3,1; 3,3). Portanto,
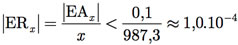
Os valores calculados para os erros relativos das medidas x e y, nos permitem concluir que a medida x apresenta uma exatidão melhor do que a medida y.