B.5 Análise de erro nas operações aritméticas de ponto flutuante
Dada uma sequência de operações aritméticas, por exemplo, (a + b)(c - d) + e, em termos de cálculo digital, torna-se importante para nós termos noção como os erros numéricos se propagam ao longo das operações aritméticas.
O erro numérico total em operações aritméticas é composto pelo erro de armazenamento das parcelas, ou fatores, mais o erro de armazenamento dos resultados parciais das operações.
Os exemplos a seguir irão ilustrar para você estudante como os erros numéricos se propagam em operações aritméticas de ponto flutuante. Para esses exemplos, considere o sistema de ponto flutuante F (10, 4, -5, 5) e os números x = 642,8 e y = 31,67. É importante que observemos que ambos os números possuem representação exata no sistema de ponto flutuante, isto é, x = 0,6428.103 e y = 0,3167.102.
Exemplo B.6: Análise do erro na operação de adição, ou seja, em x + y. Para a operação de adição em aritmética de ponto flutuante é necessário realizar o alinhamento dos pontos decimais dos números. Para isso, a mantissa do número de menor expoente tem que ser deslocada para a direita. Esse deslocamento corresponde a um número de casas decimais igual à diferença entre os dois expoentes. Portanto, para a adição temos que
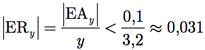
Esse é o resultado exato da adição. Como o sistema de ponto flutuante aceita apenas 4 dígitos na mantissa, o resultado da adição será:
- 0,6744.103, em caso de truncamento;
- 0,6745.103, em caso de arredondamento.
Exemplo B.7: Análise do erro na operação de multiplicação, ou seja, em x Χ y.
Para essa operação aritmética, temos que
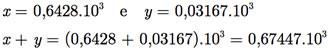
Dessa forma, no sistema de ponto flutuante dado, temos que:
- x Χ y = 0,2035.105, em caso de truncamento;
- x Χ y = 0,2036.105, em caso de arredondamento.
Os Exemplos B.6 e B.7 reforçam o que já tínhamos observado no Exemplo B.3, isto é, mesmo que os operandos estejam representados exatamente no sistema de ponto flutuante, não podemos esperar que o resultado armazenado seja exato.
Exemplo B.8: Considere os números z = 16,47 e t = 3,291. As operações de adição e multiplicação apresentam como resultados exatos
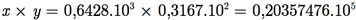
Agora, considere duas máquinas com sistema de ponto flutuante F (10, 3, -5, 5) e que armazenem os números utilizando, respectivamente, truncamento e arredondamento.
Analisemos, inicialmente, essas operações na máquina digital que realiza o armazenamento por truncamento. Nessa máquina, temos que z = 0,164.102, t = 0,329.101, x + y = 0,197.102 e x Χ y = 0,539.102. Portanto, os erros relativos são iguais a
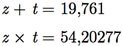
Agora, vamos analisar a máquina que realiza armazenamento por arredondamento. Nesse caso, temos que z = 0,165.102, t = 0,329.101, x + y = 0,198.102 e x X y = 0,543.102. Portanto, os erros relativos são iguais a
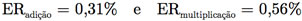
Do Exemplo B.8, podemos concluir que a máquina que realiza o armazenamento por arredondamento apresenta erros relativos menores.
Agora, chegou a hora de testarmos os nossos conhecimentos.