C.10 IDENTIDADES ENVOLVENDO CONJUNTOS
Há várias igualdades entre conjuntos envolvendo as operações de união, interseção, diferença e complementação que são válidas para quaisquer subconjuntos de um dado conjunto S. Essas igualdades são conhecidas como identidades.
A seguir, serão listadas as identidades básicas envolvendo conjuntos.
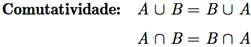
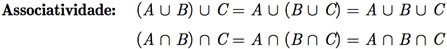
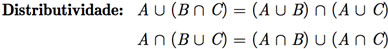

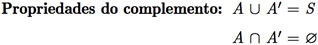
Exemplo C.9: Usando as identidades básicas entre conjuntos, mostre que a igualdade [C ∩ (A ∪ B)] ∪ [(A ∪ B) ∩ C´] = A ∪ B é verdadeira.
Vamos começar pelo lado esquerdo da igualdade. Primeiramente, utilizando a identidade da comutatividade, obtemos
[(A ∪ B) ∩ C] ∪ [(A ∪B) ∩ C´]
Agora, usando a propriedade da distributividade, obtemos
(A ∪ B) ∩ (C ∪C´)
Recordando a propriedade da operação de complemento, obtemos
(A ∪ B) ∩ S
E, finalmente, pela propriedade da existência de elemento neutro, chegamos a
A ∪ B
Prova concluída.