C.6 RELAÇÕES ENTRE CONJUNTOS
Para A = {a, e, u} e B = {a, e, i, o, u}, observamos que todo o elemento pertencente a A, também pertence a B. Nesses casos, dizemos que A é um subconjunto de B. Daí, temos que A é um subconjunto de B se (∀x)(x ∈ A → x ∈ B), que se lê “para todo x, se x pertence a A, implica que x pertence a B”.
Se o conjunto A é um subconjunto do conjunto B, escrevemos A ⊆ B. Porém, se A ⊆ B, mas A ≠ B (existe, pelo menos, um elemento em B que não pertence a A), então A é dito um subconjunto próprio de B, e escrevemos A ⊂ B.
Exemplo C.3: Considere os conjuntos A = {1, 4, 9, 16}, B = {4, 9} e C = {4, 9, 16, 25}. As seguintes proposições são todas verdadeiras.
a)B ⊆ C
b)B ⊆ A
c)B ⊂ A
d)A 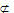 C
C
e)16 ∈ C
f){4,9} ⊆ B
g){4} ⊂ A
h)9 ∈ A
A proposição “d” significa que o conjunto A não é um subconjunto do conjunto C.
Exemplo C.4: Considere os conjuntos A = {x | x é um inteiro positivo,x ≥ 8}, B = {11, 13, 15, 17, 19} e C = {x | x é um inteiro positivo, x ≤ 22}. Determine se cada proposição a seguir é verdadeira ou falsa.
a) B ⊆ C
Verdadeira
b) B ⊂ A
Verdadeira
c) A ⊆ C
Falsa. Observe, por exemplo, que os elementos 23 e 24 pertencem a A e não pertencem a C.
d) {11, 12, 13} ⊆ A
Verdadeira
e) 6 ∈ A
Falsa. Somente os números maiores ou iguais a 8 fazem parte do conjunto A.
f) {15, 17, 19, 21, 23} ⊆ C
Falsa. Somente os números menores ou iguais a 22 fazem parte do conjunto C. Assim, o elemento 23 não pertence ao conjunto C.