C.8 OPERAÇÕES BINÁRIAS E UNÁRIAS
Inicialmente, vamos definir o termo par ordenado. Um par ordenado consiste de dois elementos quaisquer de um conjunto listados entre parênteses. Assim, um par ordenado é denotado por (x, y), onde x é a primeira componente e y é a segunda. A ordem das componentes é muito importante em um par ordenado. Assim, os conjuntos {5, 6} e {6, 5} são iguais, mas os pares ordenados (5, 6) e (6, 5) são diferentes. Nós já trabalhamos intuitivamente com essa ideia de pares ordenados como coordenadas para se localizar um ponto no plano. Por exemplo, a localização do ponto (5, 6) no plano cartesiano é completamente diferente da localização do ponto (6, 5) no mesmo plano.
Para dois pares ordenados (x, y) e (u, v), esses serão iguais se, e somente se, x = u e y = v.
Exemplo C.6: Dado o par ordenado (3x - y, x + 2y) = (10, 8), calcule os valores de x e y.
Para que haja a igualdade entre os pares ordenados, lembre que as suas respectivas coordenadas devem ser iguais. Assim, temos que
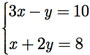
Observe que temos um sistema linear com duas incógnitas e duas equações, cuja solução é x = 4 e y = 2.
a) Definição de operação binária: uma operação em um conjunto S é uma operação binária, denotada genericamente por o, se, para todo par ordenado (x, y) de elementos de S, x º y existe, é única e pertence a S.
As condições de que x º y existe e é única equivale a dizer que a operação x º y está bem definida. A condição de que x º y sempre pertence a S é interpretada dizendo-se que S é fechado em relação à operação º.
Como exemplos de operações binárias, podemos citar as operações de adição, subtração e multiplicação no conjunto dos números inteiros Z. Assim, ao efetuarmos a operação de adição entre dois números inteiros x e y, x + y existe, é único e pertence ao conjunto Z.
Por outro lado, a operação de divisão não é uma operação binária em Z, pois x ¸ 0 não existe. Da mesma forma, a operação de subtração não é uma operação binária no conjunto dos números naturais N, pois N não é fechado em relação à subtração (1 - 2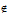 
N).
Considere a operação x º y definida em N por
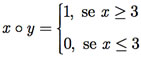
Observe que, pela primeira parte da definição de x º y, 3 º 1 = 1, porém, pela segunda parte, 3 º 1 = 0. Assim, a operação o não está bem definida em N e, por conseguinte, a operação o não é uma operação binária.
b) Definição de operação unária: uma operação em um conjunto S é uma operação unária, denotada genericamente por #, quando é verdade que x# é bem definida para todo x em S e que S é fechado em relação a #. Em outras palavras, qualquer que seja x ∈ S, x # existe, é único e pertence a S. Caso uma dessas condições falhe, não teremos uma operação unária.
Por exemplo, considere a operação unária definida por x # = -x, de modo que x # é o negativo de x. A operação # é uma operação unária no conjunto Z, entretanto, não o é em N, pois N não é fechado em relação a #.
Exemplo C.7: Quais das expressões a seguir não definem operações binárias nem unárias nos conjuntos dados? Por quê?
a)x º y = x ¸ y; S = conjunto de todos os números inteiros positivos.
Não define uma operação binária, pois S não é fechado em relação à divisão.
b)x º y = x ¸ y; S = conjunto de todos os números reais positivos.
É uma operação binária.
c)x º y = x y; S = conjunto dos números reais.
Não define uma operação binária, pois 00 não está definido.
d)x º y = máximo entre x e y; S = conjunto dos números naturais.
Define uma operação binária.
e)x # =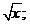 
S = conjunto de todos os números reais positivos.
Define uma operação binária.
f)x # = solução da equação (x #)2 = x; S = conjunto dos números complexos.
Não define uma operação unária, pois x # não é único para x = 4, por exemplo, 22 = 4 e (-2)2 = 4.