C.9 OPERAÇÕES COM CONJUNTOS
Para as definições a seguir, considere que A e B sejam dois subconjuntos de um determinado conjunto universo U.
União de conjuntos
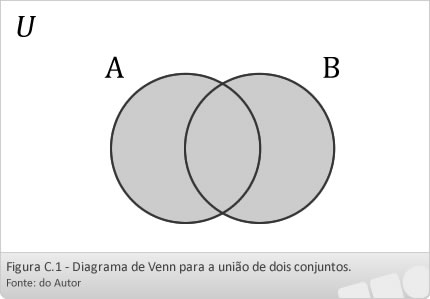
A união dos conjuntos A e B, denotada por A ∪B, é o conjunto {x | x ∈ A ou x ∈ B}. A Figura C.1 ilustra graficamente a união dos conjuntos A e B. Essa visualização é conhecida como diagrama de Venn. A área hachurada corresponde à união dos conjuntos A e B.
Interseção de conjuntos
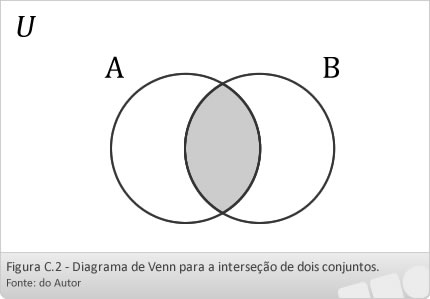
A interseção dos conjuntos A e B, denotada por A ∩ B, é o conjunto {x | x ∈A e x ∈ B}. A Figura C.2 é o diagrama de Venn para a interseção dos conjuntos A e B. A área hachurada corresponde à interseção dos conjuntos.
Complemento de um conjunto
O complemento de um conjunto A, denotado por A´ é o conjunto {x | x ∈ U e x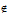 
A}. A figura C.3 ilustra o complemento do conjunto A através do diagrama de Venn. A área hachurada corresponde ao complemento do conjunto A.
Diferença entre conjuntos
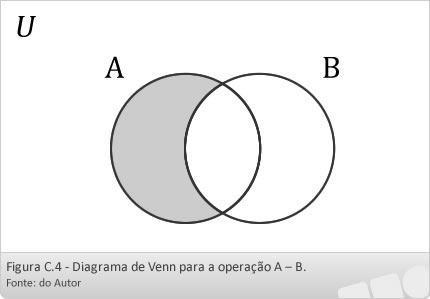
A diferença entre os conjuntos A e B, denotada por A - B, é o conjunto {x | x ∈ A e x 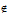B}. A Figura C.4 mostra o diagrama de Venn para a operação de diferença entre conjuntos. A área hachurada corresponde a A - B.
Conjuntos disjuntos
Dois conjuntos A e B são ditos disjuntos se A ∩ B = Ø. Assim, temos que A - B e B - A são conjuntos disjuntos.
Produto cartesiano
O produto cartesiano de dois conjuntos A e B, denotado por A X B, é o conjunto {(x, y) | x ∈ A e y ∈ B}. Assim, o produto cartesiano de dois conjuntos A e B é o conjunto de todos os pares ordenados com primeira componente em A e a segunda em B.
Exemplo C.8: Sejam os subconjuntos A = {1, 3, 5, 7} e B = {2, 3, 4, 5, 6, 8} do conjunto universo U = números inteiros positivos. Para, esses conjuntos, temos que
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
A ∩ B = {3, 5}
A´ = conjunto dos números inteiros positivos com exceção dos números 1, 3, 5 e 7
B´ = conjunto dos números inteiros positivos com exceção dos números 2, 3, 4, 5, 6 e 8
A - B = {1, 7}
B - A = {2, 4, 6, 8}
A X B = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 8), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (3, 8), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (5, 8), (7, 2), (7, 3), (7, 4), (7, 5), (7, 6), (7, 8)}
B X A = {(2, 1), (2, 3), (2, 5), (2, 7), (3, 1), (3, 3), (3, 5), (3, 7), (4, 1), (4, 3), (4, 5), (4, 7), (5, 1), (5, 3), (5, 5), (5, 7), (6, 1), (6, 3), (6, 5), (6, 7), (8, 1), (8, 3), (8, 5), (8, 7)}