Unidade D - RELAÇÕES

D.2 Relações Binárias

Definição: dado um conjunto S, uma relação binária em S é um subconjunto de S X S (um conjunto de pares ordenados de S).

Vamos recordar a Unidade C. O produto cartesiano de um conjunto S com ele mesmo, S X S, é o conjunto de todos os pares ordenados de elementos de S. Por exemplo, se S = {a, b, c}, então

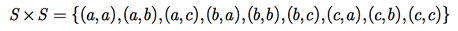
Se estivéssemos interessados na relação de igualdade, então (a, a), (b, b) e (c, c) seriam os elementos de S X S escolhidos, ou seja, os únicos pares ordenados que satisfazem a relação desejada (componentes iguais). Podemos afirmar que os pares ordenados (x, y) são aqueles que satisfazem x = y.

Assim, genericamente, podemos utilizar a notação x  y com o significado de que o par ordenado (x, y) satisfaz a relação . A relação r pode ser descrita em termos de palavras ou listando-se os pares ordenados que a satisfazem. Matematicamente, temos que

Em geral, uma relação binária é definida por uma descrição. Essa descrição caracteriza os elementos pertencentes à relação, ou seja, um predicado binário que é satisfeito por determinados pares ordenados.

Nos exemplos a seguir, considere S = {1, 2}. Então, S X S = {(1, 1), (1, 2), (2, 1), (2, 2)}.

Exemplo D.1: Seja a relação em S dada por x  y ↔ x + y é par. Então, (1, 1) ∈  e (2, 2) ∈ .

Exemplo D.2: A relação é definida em S por  = {(1, 2), (2, 2)}, então 1  2 e 2  2 são verdadeiras, porém, 1  1 não o é.

Relações entre Conjuntos Diferentes

Definição: Dados dois conjuntos S e T, uma relação binária de S para T é um subconjunto de S x T.

Exemplo D.3: Sejam S = {1, 2, 3} e T = {7, 8, 9}. O conjunto {(1, 7), (2, 8), (3, 9)} é formado por elementos de S x T, logo é uma relação binária de S para T.

Exemplo D.4: Para as relações binárias a seguir, quais entre os pares ordenados listados pertencem a relação?

a) x y ↔ y = x + 1; (1, 2), (1, 3), (2, 3), (2, 4)
  (1, 2) ∈ e (2, 3) ∈

b) x y ↔ y é múltiplo de x; (1, 2), (1, 3), (2, 3), (2, 4)
  (1, 2) ∈ , (1, 3) ∈ e (2, 4) ∈

c) x y ↔ y > x2; (1, 2), (1, 3), (2, 3), (2, 4)
  (1, 2) ∈ e (1, 3) ∈

Se é uma relação binária em S, então consiste em um conjunto de pares ordenados (x, y). Dada uma primeira componente x, ou uma segunda componente y, podem ser formados vários pares pertencentes à relação.

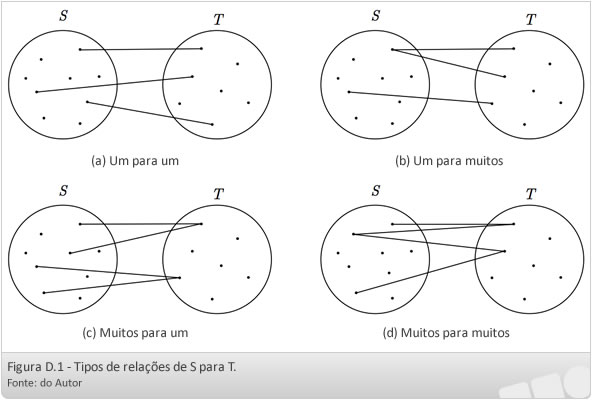
A relação é um para um se cada primeira componente e cada segunda componente aparece uma única vez na relação. A relação é um para muitos se alguma primeira componente aparece mais de uma vez. A relação é dita muitos para um se alguma segunda componente aparece mais de uma vez. E, a relação é muitos para muitos se pelo menos uma primeira componente aparece em mais de um par e pelo menos uma segunda componente aparece em mais de um par. A Figura D.1 ilustra esses tipos de relação do ponto de vista gráfico. Observe que nem todos os valores em S precisam ser componentes de algum par ordenado em .

Propriedades de Relações

Definição: Uma relação binária em um conjunto S é:

Exemplo D.5: Considere a relação de igualdade, x  y ↔ x = y, em um conjunto S.

Ela é reflexiva, pois, para qualquer x ∈ S, x = x, ou seja, (x, x) ∈ .

Ela é simétrica, pois, para quaisquer x, y ∈ S, se x = y, então y = x, ou seja, (x, y) ∈  → (y, x) ∈ .

Ela também é transitiva, pois, para quaisquer x, y, z ∈ S, se x = y e y = z, então x = z, ou seja, [(x, y) ∈ e (y, z) ∈ ] →(x, z) ∈ .

Exemplo D.6: Considere a relação “≤” no conjunto N.

Essa relação é reflexiva porque, para qualquer inteiro não-negativo x, x ≤ x.

Ela também é transitiva porque, para quaisquer x, y, z ∈ N, se x ≤ y e y ≤ z, então x ≤ z.

Porém, ela não é simétrica porque 3 ≤ 4 não implica em que 4 ≤ 3. Em verdade, para quaisquer x e y ∈ N, se x ≤ y e y ≤ x, então x = y. Essa propriedade é chamada de anti-simétrica. Matematicamente, podemos escrever que (∀x)(∀y)(x ∈S ∧ y ∈ S ∧ (x, y) ∈ r ∧ (y, x) ∈ r → x = y).

Exemplo D.7: Considere o conjunto S = {a, b, c, d}.

a)Se uma relação em S é reflexiva, quais pares ordenados pertencem à relação?
  (a, a), (b, b), (c, c), (d, d)

b)  Se uma relação em S é simétrica e se (a, b) ∈, que outros pares ordenados pertencem a ?
  (b, a)

c)  Se uma relação em S é anti-simétrica e se (a, b) ∈  e (b, a) ∈ , o que é necessário acontecer ?
  a = b

    Observação: as propriedades de simetria e anti-simetria para relações binárias não são o oposto uma da outra, como poderia parecer pelos seus nomes. Anti-simétrica não significa “não-simétrica”. Uma relação é não-simétrica se algum (x, y) pertencer à relação e (y, x) não. Portanto, as relações podem ser simétricas e anti-simétricas, anti-simétricas e não-simétricas, podem ser simétricas e anti-simétricas, ou ainda podem não ser nem simétricas nem anti-simétricas. Por exemplo, a relação de igualdade em um conjunto S é simultaneamente simétrica e anti-simétrica. Por outro lado, a relação  = {(a, e), (e, a), (a, i)} no conjunto S = {a, e, i} não é nem simétrica, (a, i) pertence à relação, porém (i, a) não; nem anti-simétrica, (a, e) e (e, a) pertencem, mas a ≠ e.

Exemplo D.8: Analise as relações binárias no conjunto S e determine se são reflexivas, simétricas, anti-simétricas ou transitivas.

a) S = N; x y ↔ x + y é par.
  é reflexiva, simétrica e transitiva.

b) S = Z+ (conjunto dos números inteiros positivos); x y ↔ x divide y.
  é reflexiva, anti-simétrica e transitiva.

c) S = conjunto de todas as retas no plano; x y ↔ x é paralela a y ou x coincide com y.
  é reflexiva, simétrica e transitiva.

d) S = N; x y ↔ x = y2.
  é anti-simétrica.

e) S = {0, 1}; x y ↔ x = y2.
  é reflexiva, simétrica, anti-simétrica e transitiva.

f) S = {x | x é uma pessoa que mora em Passo Fundo}; x y ↔ x é mais velho do que y.
  é anti-simétrica e transitiva.

g) S = {x | x é um aluno em sua turma}; x y ↔ x senta-se na mesma fila que y.
  é reflexiva, simétrica e transitiva.

h) S = {a, b, c}; r = {(a, a), (b, b), (c, c), (a, b), (b, a),}.
  é reflexiva, simétrica e transitiva.