D.3 Ordens Parciais
Definição: uma relação binária em um conjunto S que seja reflexiva, anti-simétrica e transitiva é denominada de ordem parcial em S.
Para ilustrar a definição anterior, as relações a seguir são ordens parciais.
a) Em N; x 
y ↔ x ≤ y
b) Em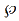 
;(N); A B ↔ A ⊆ B
c) Em Z+; x y ↔ x divide y
d) Em {0, 1}; x y ↔ x = y2
Se é uma ordem parcial em S, então o par ordenado (S, ) é denominado conjunto parcialmente ordenado. Utilizaremos a notação (S, x) para um conjunto parcialmente ordenado qualquer.
Seja (S, x) um conjunto parcialmente ordenado. Se x x y, então ou x = y ou x ≠ y. Se x x y mas x ≠ y, escrevemos x y e dizemos que x é um predecessor de y ou que y é um sucessor de x. Um dado y pode ter muitos predecessores, mas se x y e se não existe nenhum z com x z y, então x é um predecessor imediato de y.
Exemplo D.9: Considere a relação “x divide y” em {1, 2, 3, 6, 12, 18}.
a) Escreva os pares ordenados (x, y) pertencentes à relação.
(1, 1), (1, 2), (1, 3), (1, 6), (1, 12), (1, 18), (2, 2), (2, 6), (2, 12), (2, 18), (3, 3), (3, 6),
(3, 12), (3, 18), (6, 6), (6, 12), (6, 18), (12, 12), (18, 18).
b) Escreva os predecessores de 6.
1, 2, 3
c) Escreva os predecessores imediatos de 6.
2, 3
Se S for finito, podemos representar visualmente um conjunto parcialmente ordenado (S, x) por um diagrama de Hasse. Cada elemento de S é representado por um ponto, denominado nó ou vértice do diagrama. Se x é um predecessor imediato de y, o nó que representa y é colocado acima do nó que representa x e os dois nós são ligados por um segmento de reta.
Exemplo D.10: considere 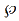({1, 2}) com a relação de inclusão de conjuntos. Esse é um conjunto parcialmente ordenado. Os elementos de 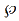({1, 2}) são 
, {1}, {2} e {1, 2}. A relação binária ⊆ consiste nos seguintes pares ordenados:
(, ), (, {1}), (, {2}), (, {1, 2}), ({1}, {1}), ({1}, {1, 2}),
({2}, {2}), ({2}, {1, 2}), ({1, 2}, {1, 2})
O diagrama de Hasse desse conjunto parcialmente ordenado está mostrado na Figura D.2. É importante observar que embora não seja um predecessor imediato de {1, 2}, ele é um predecessor de {1, 2}.
Exemplo D.11: Construa o diagrama de Hasse para o conjunto parcialmente ordenado do Exemplo D.9.
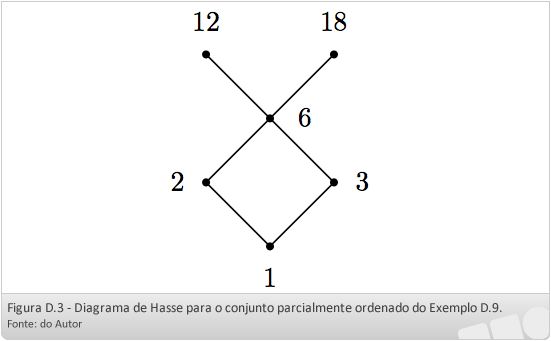
O diagrama de Hasse de um conjunto parcialmente ordenado contém todas as informações sobre a ordem parcial. Assim, podemos obter o conjunto de pares ordenados a partir do diagrama. Os segmentos de reta indicam os predecessores e sucessores. Podemos completar o resto utilizando as propriedades da reflexividade e da transitividade.
Exemplo D.12: Determine o conjunto de pares ordenados da ordem parcial dada pelo seu diagrama de Hasse (Figura D.4).
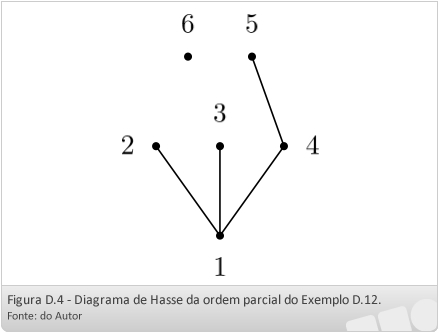
O conjunto dos pares ordenados da ordem parcial são
{(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (1, 2), (1, 3), (1, 4), (1, 5), (4, 5)}