Unidade D - RELAÇÕES

D.4 Relações de Equivalência

Definição: uma relação binária em um conjunto S que seja reflexiva, simétrica e transitiva é denominada de relação de equivalência em S.

Exemplos de relações de equivalência:

a) Em qualquer conjunto S, x r y ↔ x = y.
b) Em N, x y ↔ x + y é par,
c) No conjunto de todas as retas no plano, x y ↔ x é paralela ou coincide com y.
d) Em {0, 1}, x y ↔ x = y².
e) Em {x | x é um aluno em sua turma}, x y ↔ x senta-se na mesma fila que y.
f) Em {a, b, c}, = {(a, a), (b, b), (c, c), (a, b), (b, a)}.

Iremos abordar agora uma característica importante das relações de equivalência. Considere o exemplo “e” acima. Ao agruparmos todos os alunos no conjunto S que estão relacionados entre si, chegamos à Figura D.5. Nós dividimos o conjunto S em subconjuntos de modo que todos na turma pertencem a um, e apenas um, subconjunto.

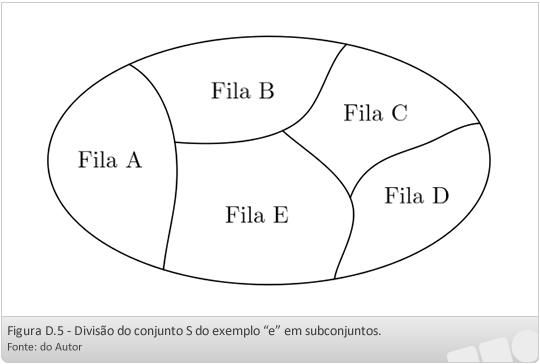
Definição: uma partição de um conjunto S é uma decomposição de S em subconjuntos não vazios tais que todo o elemento de S pertence a um, e apenas um, desses subconjuntos. A cada um desses subconjuntos chamamos elementos da partição.

Assim, qualquer relação de equivalência divide o conjunto onde está definida em uma partição. Os subconjuntos que compõem a partição são formados agrupando-se os elementos relacionados.

Se é uma relação de equivalência em um conjunto S e se x ∈ S, denotamos por [x] o conjunto de todos os elementos relacionados a x em S e esse conjunto é chamado de classe de equivalência de x. Portanto,

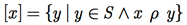
 No caso do exemplo “e” anterior, suponha que os alunos Antônio, Carla, José e Bianca sentem na mesma fila. Então, [Antônio] = {Carla, José, Bianca}. Temos ainda que [Antônio] = [Carla] = [José] = [Bianca]. Essas não são classes distintas, mas a mesma classe com diferentes nomes. Uma classe de equivalência pode usar o nome de qualquer um dos seus elementos.

Teorema: uma relação de equivalência r em um conjunto S define uma partição de S e uma partição de S define uma relação de equivalência em S.

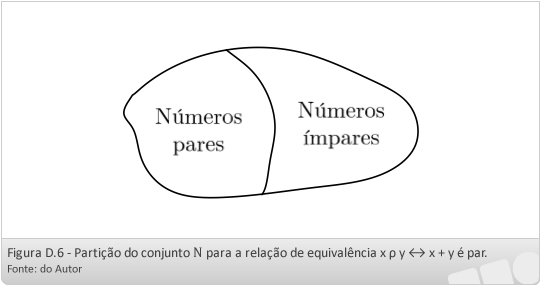
Exemplo D.13: vamos considerar a relação de equivalência em N, x y ↔ x + y é par. Essa relação divide o conjunto N em duas classes de equivalência. Se x é um número par, então, para todo o número par y, x + y é par e y ∈ [x]. Todos os números pares formam uma classe de equivalência. Por outro lado, se x é ímpar, então, para todo o número ímpar y, x + y é par e y ∈ [x]. Todos os números ímpares formam a segunda classe de equivalência. A partição pode ser representada como mostrado na Figura D.6.

Observe que uma classe de equivalência pode ter mais de um nome. No Exemplo D.13, [2] = [100] = [1048] e [1] = [277] = [2359].

Exemplo D.14: No conjunto {a, b, c}, r = {(a, a), (b, b), (c, c), (a, b), (b, a)}, descreva as classes de equivalência.

[a] = [b] = {a, b} e [c] = {c}

A Tabela D.1 apresenta um resumo sobre as características importantes de ordens parciais e de relações de equivalência.

Tipo de relaÇÃo binÁria	Reflexiva	SimÉtrica	Anti-simÉtrica	Transitiva	CaracterÍstica importante
Ordem parcial	Sim	Não	Sim	Sim	Predecessor e sucessor
Relação de equivalência	Sim	Sim	Não	Sim	Determina uma partição