E.1 Introdução
Nessa unidade, nós vamos tratar de um caso especial de relações binárias de um conjunto S em um conjunto T: as funções. Funções são relações binárias nas quais para todo elemento do conjunto S corresponde um único elemento do conjunto T.
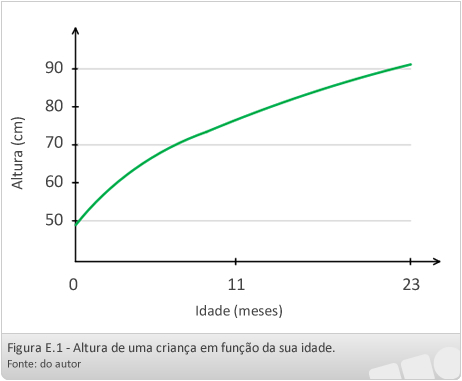
Função é uma expressão muito comum no nosso dia a dia. Imagine, por exemplo, uma revista que apresente uma reportagem sobre o crescimento de crianças. A reportagem poderia dizer que “A altura de uma criança depende da sua idade” ou “A altura de uma criança é função da sua idade”. Essa relação funcional pode ser expressa graficamente, como mostrada na Figura E.1. A figura explica que, quanto mais idade a criança tiver, maior será a sua altura.
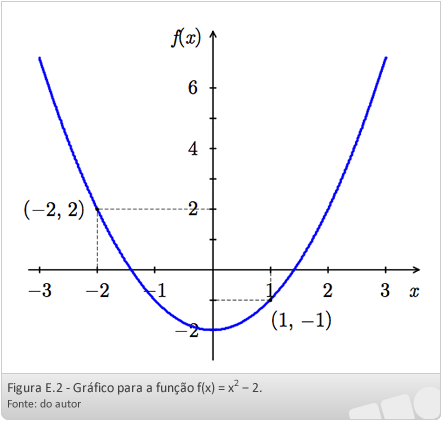
Nós também utilizamos as funções matemáticas em álgebra e cálculo. Por exemplo, a equação f(x) = x2 - 2 expressa uma relação funcional entre os valores de x e os de f, quando x é substituído por seu valor na expressão de f. Assim, para x = -2, f(-2) = 2. De forma semelhante, f(1) = -1, e assim por diante. Observe que para cada valor de x, f(x) é único. Ainda, temos que, se x puder assumir qualquer valor real, o gráfico resultante para a função f(x) está mostrado na Figura E.2.
Dos exemplos apresentados, constatamos que existem três partes em uma função:
- um conjunto de valores iniciais ou domínio da função;
- um conjunto com os valores associados ou contradomínio da função;
- a associação propriamente dita.
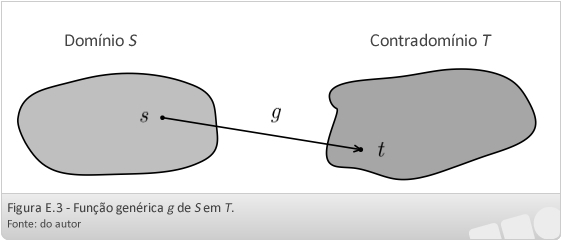
A Figura E.3 apresenta uma função qualquer g. Nela, g é uma função de S em T, simbolizada por g:S -> T. S é o domínio e T é o contradomínio. A associação é um conjunto de pares ordenados da forma (s, t), onde s ∈ S e t ∈ T, ou seja, t = g(s). Assim, observamos que a associação é um subconjunto de S X T (uma relação binária de S em T).