E.2 Terminologia para Funções
Sejam S e T conjuntos. Uma função f de S em T, f:S -> T, é um subconjunto de S x T tal que cada elemento de S aparece exatamente uma vez como a primeira componente de um par ordenado. S é o domínio e T é o contradomínio da função. Se (s, t) pertence à função, então denotamos t por f(s), t é a imagem de s sob f, s é uma imagem inversa de t sob f e f leva s em t.
Uma função de S em T é um subconjunto de S x T com algumas restrições sobre os pares ordenados que a compõem. Por esse motivo, dizemos que uma função é um tipo particular de relação binária. Pela definição de função, uma relação do tipo um para muitos (ou muitos para muitos) não pode ser uma função. Além disso, cada elemento de S tem que aparecer como primeira componente.
Exemplo E.1: Quais das relações a seguir são funções? Para as que não são, por que não?
a) g:S -> T, onde S = T = {a, b, c} e g = {(a, a), (b, c), (c, a), (b, a)}
Não é função, pois existem dois valores associados a b ∈ S.
b) g:Z -> N, onde g(x) = |x|
É função.
c) g:N -> N, onde g(x) = x - 2
Não é função, pois para os valores 0 e 1 do domínio, os valores correspondentes de g(x) não pertencem ao contradomínio.
d) g:S -> T, onde S é o conjunto de pessoas em sua família, T é o conjunto de todos os números de RG e g associa cada pessoa ao seu RG
Não é função, pois nem todas as pessoas de sua família possuem RG (por exemplo, as crianças pequenas)
e) g:S -> T, onde S é o conjunto de todos os polinômios de grau 2 em x com coeficientes inteiros, T = Z e g(x) = a + b + c
É função
f) g:R ® R, onde g(x) = 12x + 5
É função
g) g:N -> N, onde g é definida por
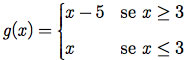
Não é função, pois existem dois valores associados a 3 ∈ N
A definição de função inclui funções em mais de uma variável. Podemos ter uma função f:S1 x S2 x ... x Sn -> T que associa a cada n-upla de elementos (s1, s2, ..., sn), si ∈ S, um único elemento em T.
Por exemplo, seja a função g:Z x N x {3, 4} → Z dada por g(x, y, z) = yz - x. Então, g(-2, 3, 4) = 34 - (-2) = 83 + 2 = 83.