E.4 Composição de Funções
Considere que f e g são funções, com f:S → T e g:T → U. Então, para todo s ∈ S, f(s) = t é um elemento de T, que é o contradomínio de f. Logo, a função g pode ser calculada em f(s). O resultado é g(f(s)) = u, que é um elemento de U. A Figura E.5 ilustra o procedimento descrito.
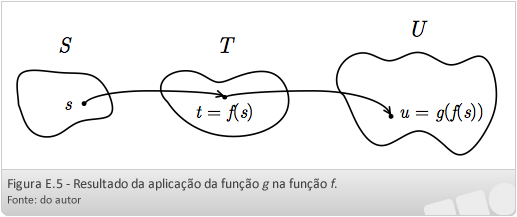
Resumindo o procedimento anterior, podemos dizer que escolhemos um elemento arbitrário s em S, aplicamos a função f neste elemento e, depois, aplicamos a função g a f(s). Isso é a mesma coisa que associar um elemento de U a s. Assim, nós criamos uma função S → U, denominada composição das funções f e g e denotada por g o f. A Figura E.6 ilustra o descrito.
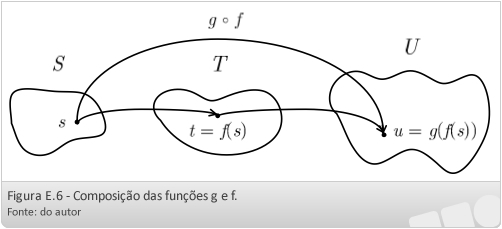
Definição: Sejam as funções f:S → T e g:T → U. A função composta g o f é a função de S em U definida por (g o f)(s) = g(f(s)).
Observe que a função g o f é aplicada da esquerda para a direita; primeiro aplicamos a função f e, após, a função g.
Exemplo E.2: Sejam as funções f:N → N definida por f(x) = x + 3 e g:N → N definida por g(x) = x2.
a)Qual o valor de (g o f)(2)?
(g o f)(2) = g(f(2)) = g(2 + 3) = g(5) = 52 = 25
b)Qual o valor de (f o g)(2)?
(f o g)(2) = f(g(2)) = f(22) = f(4) = 4 + 3 = 7
Teorema: A composição de duas funções bijetoras é também uma função bijetora.