E.5 Funções Inversas
As funções bijetoras apresentam uma propriedade importante. Seja f:S → T uma bijeção. Como f é sobrejetora, todo t ∈ T tem uma imagem inversa s ∈ S. Como f é injetora, essa imagem inversa é única. Assim, podemos associar a cada elemento t ∈ T um único elemento s ∈ S, lembrando que t = f(s). Esse procedimento descreve uma função g:T → S. A Figura E.7 ilustra as funções f e g.
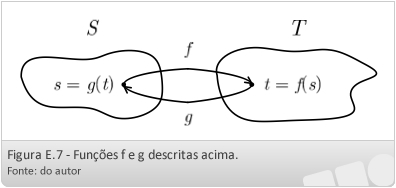
Observe que os domínios e os contradomínios de f e g são tais que podemos formar tanto g o f:S → T como f o g:T → S. Se s ∈ S, então (g o f)(s) = g(f(s)) = g(t) = s. Logo, g o f leva cada elemento de S nele mesmo.
Definição: Uma função f que leva cada elemento de um conjunto S em si mesmo é denominada de função identidade e é denotada por iS.
Assim, em relação às funções f e g anteriores, temos que f o g = iT e g o f = iS.
Definição: Seja f uma função, f:S → T. Se existir uma função g:T → S tal que g o f = iS e f o g = iT, então g é chamada de função inversa de f e denotada por f-1.
E.5.1 Teorema Sobre Bijeções e Funções Inversas
Seja f:S → T, então, f é uma função bijetora se, e somente se, f -1 existir.
Em outras palavras, podemos concluir que, se a função f é bijetora, isso equivale a dizer que a função f possui inversa.
Exemplo E.3: Considere a função f:R → R dada por f(x) = 2x + 5. Determine f -1.
f -1:R → R, com f -1(x) = (x - 5) / 2.
Resumindo o que estudamos sobre funções até o momento, a Tabela E.1 apresenta um breve sumário sobre as terminologias utilizadas no estudo de funções.
ExpressÃo |
Significado |
Função |
Aplicação de um conjunto em outro que leva cada elemento do conjunto inicial em exatamente um elemento do conjunto de chegada |
Domínio |
Conjunto inicial de uma função |
Contradomínio |
Conjunto de chegada de uma função |
Imagem |
Ponto que resulta da aplicação de uma função |
Imagem inversa |
Ponto inicial sobre o qual a função é aplicada |
Sobrejetora |
A imagem é todo o contradomínio; todo elemento no contradomínio possui uma imagem inversa |
Iinjetora |
Dois elementos no domínio não podem ser levados ao mesmo ponto no contradomínio |
Bijetora |
Quando a função é injetora e sobrejetora simultaneamente |
Função identidade |
Leva cada elemento de um conjunto em si mesmo |
Função inversa |
Para uma função bijetora, é uma função que leva cada elemento no contradomínio de volta ao elemento de onde ele veio |
Tabela E.1 Terminologias utilizadas no estudo de funções.