Unidade E - FUNÇÕES

E.6 Permutações

As funções bijetoras de um conjunto em si mesmo possuem um nome especial.

Definição de Permutações de um Conjunto: Para um dado conjunto A, SA = {f | f:A → A é uma função bijetora}. SA é, portanto, o conjunto de todas as funções bijetoras do conjunto A em si mesmo; essas funções são denominadas de permutações de A.

Assim, se f e g pertencem a SA, então cada uma delas tem o domínio igual à imagem e igual ao próprio conjunto A. Além disso, como f e g são bijetoras, pelo teorema sobre a composição de funções bijetoras, g o f também é bijetora, ou seja, leva a um único elemento de SA. Daí, podemos concluir que a composição de funções é uma operação binária no conjunto SA.

Notação para permutações

As funções permutações representam arranjos ordenados de objetos no domínio. Dessa forma, uma das maneiras de descrevê-las é na forma de um arranjo retangular, onde os elementos do domínio ficam na linha de cima e os elementos da imagem ficam diretamente abaixo desses elementos.

Por exemplo, considere o conjunto A = {a, b, c, d} e uma função permutação em A, f, dada por f = {(a, b), (b, c), (c, a), (d, d)}. A sua representação na forma de um arranjo retangular é

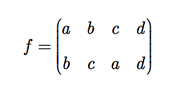
Observe que a linha de baixo é um arranjo ordenado dos objetos na linha de cima.

Outra maneira de descrever uma função permutação é com a notação de ciclo. Nessa, os elementos são listados um ao lado do outro, de modo que a função leva cada elemento ao que está imediatamente a sua direita e o último elemento na lista leva ao primeiro. Nessa notação, qualquer elemento que não apareça na lista significa que leva a si mesmo. Por exemplo, seja a função permutação f dada anteriormente. A sua notação de ciclo é f = (a, b, c). Aqui, a leva a b, b leva a c, c leva a a e d leva em si mesmo.

Exemplo E.4: Sejam A = {a, b, c, d, e} e f ∈ S_A dada por

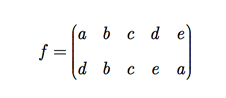
Escreva f em forma de ciclo.

f = (a, d, e)

Exemplo E.5: Sejam A = {a, b, c, d, e} e g ∈ S_A dada por g = (b, d, e, c). Escreva g na forma de arranjo retangular.

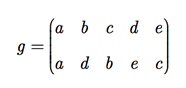
Exemplo E.6: Considere A = {a, b, c, d} e f, g ∈ S_A dadas por f = (a, b, c) e g = (b, c). Determine a função composta g o f.

Inicialmente, vamos verificar o que acontece com o elemento a em A. Operando da direita para a esquerda (primeiro f, depois g), temos a → b sob f e, depois, b → c sob g. Assim, a  → c sob g o f. De forma semelhante, b → c sob f e c → b sob g. Então, b → b sob sob g o f. Analogamente, temos c → a sob f e a → a sob g. Então, c -> a sob sob g o f. e, finalmente, d → d sob f e d → d sob g. Então, d → d sob sob g o f. Concluindo, temos que g o f = (a, c).

Teorema: Seja m o número de elementos no conjunto S (|S| = m) e n o número de elementos no conjunto T (|T| = n). Então:

1. O número de permutações de S é P_S = m! e o de T é P_T = n!.

2. O número de funções f:S →T é n^m.
3. Supondo que m ≤ n, o número de funções injetoras f:S → T é  
   
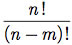
4. Supondo que m ≥ n, o número de funções sobrejetoras f:S → T é <IMAGEM>
   onde C(r, s) são as combinações de a elementos em grupos de b elementos, ou seja,
   

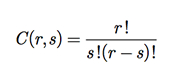
Exemplo E.7: Sejam os conjuntos A = {1, 2, 3} e B = {4, 5}. Determine:

a)o número de permutações P_A e P_B, respectivamente, nos conjuntos A e B;
b)o número de funções sobrejetoras nfs de A em B.

Temos que |A| = 3 e |B| = 2. Então, pelo teorema anterior, obtemos

a)PA = 3! = 3 x 2 x 1 = 6
  PB = 2! = 2 x 1 = 2

b)nfs = 23 - C(2, 1)(1)³ = 8 - 2 x 1 = 6