E.8 Ordem de Grandeza de Funções
A ordem de grandeza é uma forma de compararmos a “taxa de crescimento” de funções distintas. Pela nossa prática, sabemos que se calcularmos f(x) = x e g(x) = x2 para valores cada vez maiores de x, os valores de g serão maiores do que os valores de f, e a diferença aumenta cada vez mais. Essa diferença não vai deixar de existir se multiplicarmos os valores de f por uma constante muito grande; não importa o tamanho da constante, em algum momento os valores de g certamente começarão a ficar maiores do que os de f. Para caracterizarmos essa diferença, definiremos uma relação binária nas funções.
Seja S o conjunto de todas as funções com domínio e contradomínio iguais aos números reais não-negativos. Podemos definir uma relação binária em S por
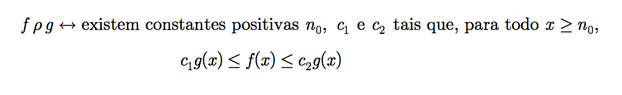
Exemplo E.8: Considere as funções f e g pertencentes a S, com f(x) = 5x2 e g(x) = 100x2 +100x + 25. Sejam n0 = 1, c1 = 1/100 e c2 = 1. Portanto, para x ≥ 1, temos
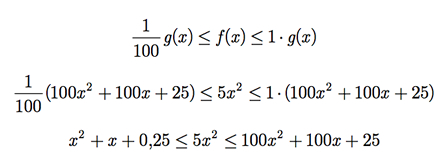
Portanto, f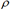 
g.
Exemplo E.9: Para os valores de x iguais a 2, 3, 4 e 5, verifique a desigualdade do Exemplo E.8.
a)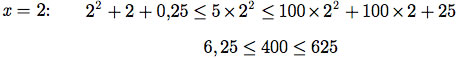 
b)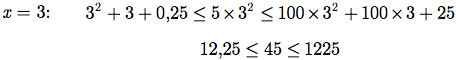 
c)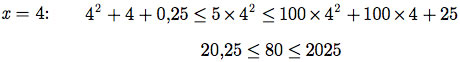 
d)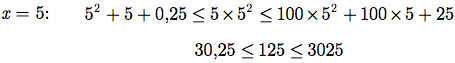 
Exemplo E.10: Determine um novo conjunto de valores para n0, c1 e c2 que também comprovam f 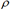g no Exemplo E.8.
Considere n0 = 1, c1 = 1/200 e c2 = 1. Portanto, para x ≥ 1, temos
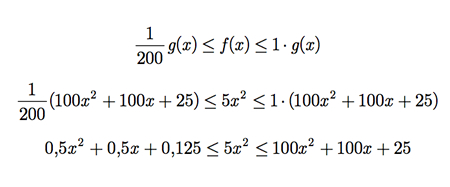
Exemplo E.11: Demonstre que 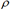é simétrica e transitiva.
a) Admita f 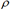g. Logo, existem constantes positivas n0, c1 e c2 tais que, para todo x ≥ n0, c1g(x) ≤ f(x) ≤ c2g(x). Portanto, para x ≥ n0, (1/c2)f(x) ) ≤ g(x) ≤ (1/c1)f(x), de modo que g 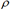f.
b) Admita f 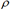g e g 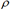h. Então, existem constantes positivas n0, n1, c1 , c2, d1 e d2 tais que, c1g(x) ≤ f(x) ≤ c2g(x) para x ≥ n0 e d1h(x) ≤ g(x) ≤ d2h(x) para x ≥ n1. Portanto, para x ≥ max(n0, n1), c1d1h(x) ≤ f(x) ≤ c2d2h(x), de modo que f 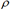h.
Definição: Sejam f e g funções dos reais não-negativos nos reais não-negativos. Então, f tem a mesma ordem de grandeza que g, denotada por f = Q(g), se existem constantes positivas n0, c1 e c2 tais que, se x ≥ n0, c1g(x) ≤ f(x) ≤ c2g(x).