F.2 O Princípio da Multiplicação
Inicialmente, considere a seguinte situação. Um estudante pode escolher um entre dois lápis, um HB e outro 2B, e uma entre três canetas, uma azul (A), outra preta (P) e outra vermelha (V). Quantos conjuntos diferentes o estudante pode ter?
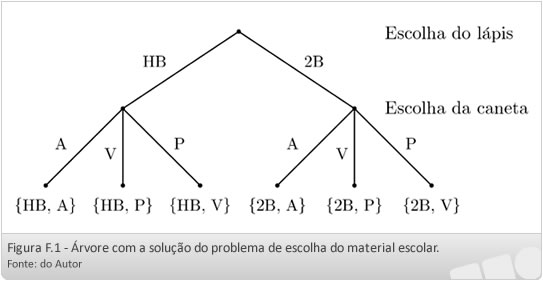
Podemos resolver esse problema separando a tarefa de escolha do material escolar em duas etapas sequenciais: escolher, primeiro, o lápis e, depois, a caneta. A árvore da Figura F.1 mostra que existem 2 x 3 = 6 possibilidades: {HB, A}, {HB, P}, {HB, V},{2B, A},{2B, P} e {2B, V}.
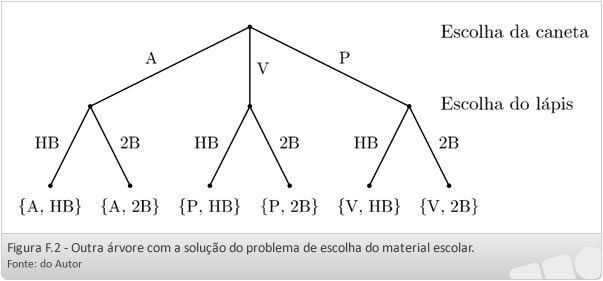
Nesse problema, a ordem dos eventos poderia ser trocada: o estudante poderia, primeiro escolher a caneta e, depois, o lápis. A Figura F.2 mostra a árvore de decisão. Observe que o número de possibilidades não se altera (3 x 2 = 6).
O problema da escolha do material escolar ilustra o fato de que o número total de resultados possíveis para uma sequência de eventos pode ser obtido multiplicando-se o número de possibilidades do primeiro evento pelo número de possibilidades do segundo.
Princípio da Multiplicação: Se existem n1 resultados possíveis para um primeiro evento e n2 para um segundo, então existem n1 x n2 resultados possíveis para a sequência dos dois eventos.
O princípio da multiplicação é útil sempre que quisermos contar o número total de possibilidades para uma tarefa que pode ser dividida em uma sequência de etapas sucessivas.
Exemplo F.1: A última parte de um número telefônico é composta por quatro dígitos. Quantos desses números existem?
Podemos formar números com quatro dígitos através de uma sequência de tarefas: escolher o primeiro dígito, depois o segundo, depois o terceiro e, finalmente, o quarto. Temos 10 dígitos disponíveis (de 0 a 9) para cada posição. Assim, temos 10 possibilidades para a primeira tarefa, 10 para a segunda, 10 para a terceira e 10 para a quarta. Portanto, temos que o total de números com quatro dígitos é 10 x 10 x 10 x 10 = 10.000.
Exemplo F.2: Em relação ao Exemplo F.1, quantos números de quatro dígitos existem se um mesmo dígito não puder ser repetido?
Novamente temos uma sequência de tarefas. Só que agora não podemos ter repetições. Assim, temos 10 possibilidades para o primeiro dígito, 9 para o segundo, 8 para o terceiro e 7 para o quarto. Portanto, o número total de possibilidades é 10 x 9 x 8 x 7 = 5.040.