F.5 Princípio de Inclusão e Exclusão
Inicialmente, vamos observar que, se A e B são subconjuntos de um conjunto universo S, então A - B, B - A e A ∩ B são disjuntos dois a dois. Isso significa que, se x ∈ A - B, então x  B - A e x
B - A e x  A ∩ B. A Figura F.3 ilustra esse fato.
A ∩ B. A Figura F.3 ilustra esse fato.
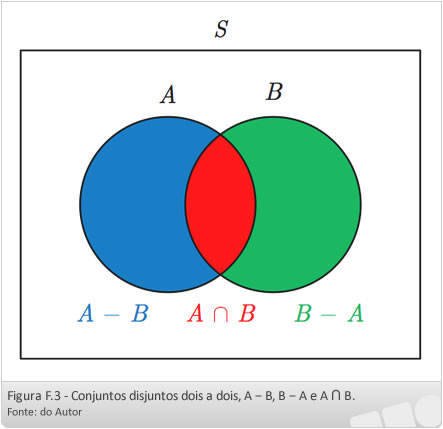
Observando a Figura F.3, podemos deduzir outros pontos importantes em relação ao número de elementos em cada subconjunto. Notamos que
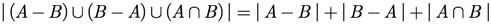
(F.1) e
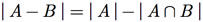
(F.2) e
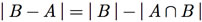
(F.3)
Ainda, pela análise da Figura F.3, podemos concluir que
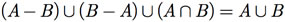
(F.4)
Usando as expressões(F.2),(F.3) , e(F.4) na equação , obtemos que
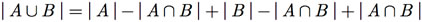
ou
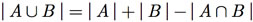
(F.5)
A equação (F.5) é o princípio de inclusão e exclusão para dois conjuntos. O nome deriva do fato de que, ao contar o número de elementos na união de A e B, precisamos somar (incluir) o número de elementos de A e o número de elementos de B e precisamos subtrair (excluir) o número de elementos de A ∩ B, para evitar contá-los duas vezes.
Exemplo F.8: Uma pesquisa eleitoral entrevistou 100 eleitores, todos apoiando o candidato 1, o candidato 2 ou ambos, e descobriu que 45 eleitores apóiam o candidato 1 e 63 apóiam o candidato 2. Quantos eleitores apóiam ambos os candidatos?
Denotando por A o conjunto dos eleitores que apóiam o candidato 1 e por B o conjunto dos eleitores que apóiam o candidato 2, temos que |A ∪ B| = 100, |A| = 45 e |B| = 63. Utilizando a equação (F.5), temos que
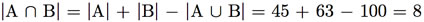
Portanto, há 8 eleitores que apóiam ambos os candidatos.
A equação (F.5) pode ser estendida a três conjuntos, como a seguir.
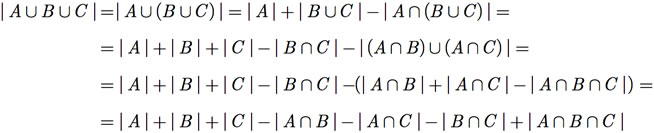
Portanto, a versão do princípio de inclusão e exclusão para três conjuntos é
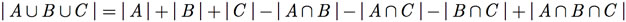
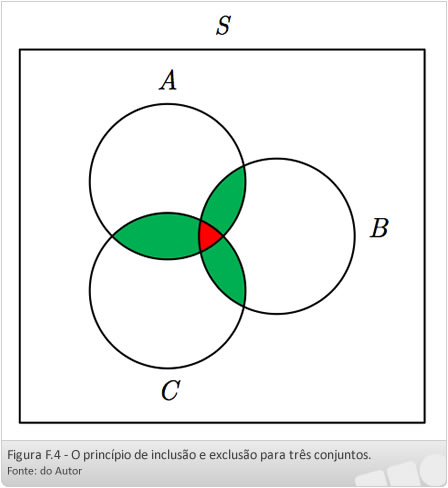
A Figura F.4 apresenta uma demonstração geométrica para |A ∪ B ∪ C|. Quando somamos |A| + |B| + |C|, estamos contando cada elemento em |A ∩ B|, |A ∩ B| e |B ∩ C| duas vezes, de modo que devemos retirar cada um deles uma vez. Por outro lado, quando somamos |A| + |B| + |C|, estamos contando cada elemento de |A ∩ B ∩ C| três vezes, mas ao subtrair |A ∩ B|, |A ∩ C| e |B ∩ C|, eliminamos três vezes esses elementos, logo precisamos colocá-los de volta uma vez.
Exemplo F.9: Um grupo de estudantes planeja comprar canetas. Desses, 15 preferem canetas azuis, 12 preferem canetas pretas, 8 preferem canetas verdes, 6 podem usar canetas azuis ou pretas, 4 podem usar tanto canetas azuis como verdes, 5 usam tanto canetas pretas quanto verdes e 2 não se importam de usar qualquer cor de caneta. Quantos estudantes há no grupo?
Por uma questão de ordem, façamos:
A = conjunto dos estudantes que usam canetas azuis
B = conjunto dos estudantes que usam canetas pretas
C = conjunto dos estudantes que usam canetas verdes
Dessa forma, temos que |A| = 15, |B| = 12, |C| = 8, |A ∪ B| = 6, |A ∪ C| = 4, |B ∪ C| = 5 e |A ∪ B ∪ C| = 2. Pelo princípio de inclusão e exclusão, temos que
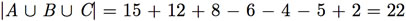
Portanto, existem 22 estudantes no grupo.
Exemplo F.10: Uma pizzaria vende três tipos de pizza: calabresa, de queijo e portuguesa. Em um determinado dia, a pizzaria atendeu 251 clientes. Desses, 127 clientes comeram pizza calabresa, 187 comeram pizza de queijo, 38 comeram pizza portuguesa, 56 comeram pizzas calabresa e de queijo, 44 comeram pizzas de queijo e portuguesa e 8 comeram os três tipos de pizza. Quantos clientes comeram pizzas calabresa e portuguesa?
Façamos:
A = conjunto dos clientes que comeram pizzas calabresas
B = conjunto dos clientes que comeram pizzas de queijo
C = conjunto dos clientes que comeram pizzas portuguesas
Dessa forma, sabemos que |A ∪ B ∪ C| = 251, |A| = 127, |B| = 187, |C| = 38, |A ∩ B| = 56, |B ∩ C| = 44 e |A ∩ B ∩ C| = 8. Pelo princípio de inclusão e exclusão, temos que
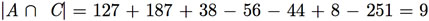
Portanto, 9 pessoas comeram pizzas calabresa e portuguesa.
Definição do Princípio de Inclusão e Exclusão: Dados conjuntos finitos A1, A2, ..., An, com n ≥ 2, tem-se que
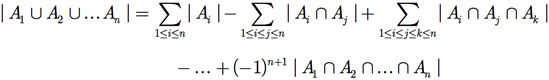
(F.7)