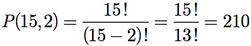F.7 Permutações
No Exemplo F.2, discutimos o problema de contar todas as possibilidades para os quatro últimos dígitos de um número telefônico sem repetição. Assim, observe que o número 5478 não é igual ao 4587, pois a ordem dos dígitos importa. Um arranjo ordenado de objetos é chamado de permutação. Cada um desses números telefônicos é uma permutação de 4 objetos distintos escolhidos em um conjunto de 10 objetos distintos (os dígitos). Quantas dessas permutações são possíveis? A resposta encontrada pelo princípio da multiplicação foi 10 x 9 x 8 x 7 = 5.040, ou seja, 10 escolhas para o primeiro dígito, 9 para o segundo (não são permitidas repetições de dígitos), 8 para o terceiro e 7 para o último dígito. O número de permutações de r objetos distintos escolhidos entre n objetos distintos é denotado por P(n, r). Portanto, no caso em questão, a solução pode ser expressa como P(10, 4).
É possível escrever uma fórmula para P(n, r) usando a função fatorial. Para um inteiro positivo n, n fatorial é definido por n×(n - 1)×(n - 2)×...×1 e é denotado por n!.
Definição: Dados n objetos distintos, o número de possibilidades de agrupá-los em grupos de r objetos distintos é
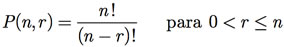
Exemplo F.13: Quantas palavras de três letras (mesmo que sem sentido) podem ser formadas a partir da palavra “software” se nenhuma letra pode ser repetida?
Observe que, nesse caso, a ordem das letras faz diferença. Assim, estamos interessados em determinar o número de permutações de três objetos distintos em um conjunto de 8 objetos distintos (as letras da palavra “software”). Portanto, queremos P(8, 3).
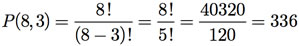
Exemplo F.14: Vinte e cinco atletas competem em uma olimpíada em um determinado esporte. Serão premiados os três primeiros colocados com medalhas de ouro, prata e bronze, respectivamente. De quantos modos diferentes essas medalhas poderão ser distribuídas?
A ordem em que as medalhas serão entregues aos atletas é importante, ou seja, o atleta A receber medalha de ouro, o B de prata e o C de bronze é diferente do atleta C receber medalha de ouro, o A de prata e o B de bronze. Assim, estamos querendo determinar o número de permutações de três objetos (as medalhas) em um conjunto de 25 atletas.
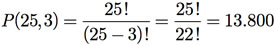
Exemplo F.15: De quantas maneiras diferentes podemos selecionar um zagueiro e um atacante em um grupo de 15 jogadores?