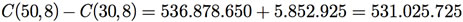F.8 Combinações
Às vezes, queremos selecionar r objetos de um conjunto de n objetos, porém não nos importamos com a ordem. Nesse caso, estamos contando o número de combinações de r objetos distintos escolhidos entre n objetos distintos, que usaremos a notação C(n, r). Para cada uma das combinações, existem r! maneiras de ordenar os r objetos escolhidos. Pelo princípio da multiplicação, o número de permutações de r objetos distintos escolhidos entre n objetos é o produto do número de escolhas possíveis dos objetos, C(n, r), pelo número de maneiras de ordenar os objetos escolhidos, r!, portanto
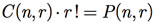
ou
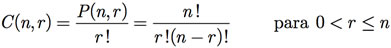
Exemplo F.16: Em uma caixa, temos 14 bolas numeradas de 1 a 14. De quantas maneiras podemos retirar grupos com três bolas?
Observe que a ordem numérica das bolas não é importante. Assim, temos um problema típico de combinações, isto é, C(14, 3).
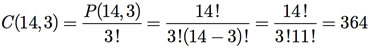
Exemplo F.17: Considere o Exemplo F.14. Suponha, agora, que queiramos saber apenas de quantas maneiras três atletas podem ser premiados nos três primeiros lugares.
Observe que, agora, a ordem em que os atletas serão premiados não é mais importante. Portanto, a solução é
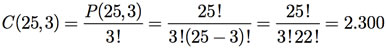
Exemplo F.18: De quantas maneiras é possível escolher uma comissão de 4 pessoas em um grupo de 10 pessoas?
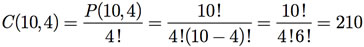
|
||||
|
Exemplo F.19: Em uma escola, desejamos formar uma comissão de dez estudantes escolhida entre duas turmas com 20 estudantes (Turma A) e 30 estudantes (Turma B). Pergunta-se:
a) De quantas maneiras é possível selecionar 4 estudantes da Turma A e 6 da Turma B?
b) De quantas maneiras é possível selecionar uma comissão com exatamente 1 estudante da Turma A?
c) De quantas maneiras é possível selecionar uma comissão com, no máximo, 1 estudante da Turma A?
d) De quantas maneiras é possível selecionar uma comissão com, pelo menos, 1 estudante da Turma A?
Primeiramente, observe que a ordem dos estudantes não é importante. Assim, temos problemas de combinações. Agora, vamos analisar caso a caso.
a) Aqui, temos uma sequência de duas tarefas, selecionar estudantes da Turma A e selecionar estudantes da Turma B. Assim, vamos usar o princípio da multiplicação para resolver esse problema. Para a Turma A, temos C(20, 4) e para a Turma B, C(30, 6). Portanto, a solução é
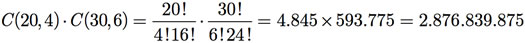
b) Novamente uma sequência de tarefas. Primeiro, selecionar um único estudante da Turma A e, depois, selecionar o restante da comissão entre os estudante da Turma B. Assim, existem C(20, 1) maneiras de se selecionar um único estudante da Turma A e C(30, 7) de se selecionar o restante da comissão entre os estudante da turma B. Portanto, a solução é
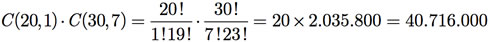
c) Agora, note que para termos, no máximo, 1 estudante da Turma A na comissão significa que podemos ter ou 1 ou 0 estudante da turma na comissão. Esses eventos são disjuntos, o que nos obriga a usar o princípio da adição. O número de maneiras de se selecionar exatamente 1 estudante da Turma A para a comissão é a resposta do item b. O número de maneiras de se selecionar 0 estudante da Turma A para a comissão é o mesmo que selecionar a comissão toda entre os estudantes da Turma B, ou seja, C(30, 8). Portanto, a solução é
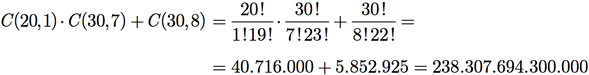
d) Há várias formas de resolver esse item. A mais simples é resolver contando todas as maneiras possíveis de se formar a comissão com 8 estudantes selecionados entre os 50 estudantes disponíveis (as turmas A e B juntas) e, depois, eliminar (subtrair) o número de comissões formadas exclusivamente por estudantes da Turma B. Logo, a resposta é