G.1 Terminologia
Os dados em muitos problemas matemáticos podem ser apresentados em forma de um arranjo retangular de valores; esse arranjo é chamado de matriz. Por exemplo,
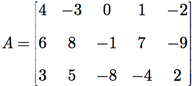
é uma matriz com três linhas e cinco colunas. A dimensão da matriz é dada pelo seu número de linhas e de colunas. No nosso exemplo, temos uma matriz com dimensão 3 X 5.
Os elementos de uma matriz A são denotados por aij, onde i é o índice da linha e j é o índice da coluna onde o elemento está. No nosso exemplo, o elemento a24 da matriz A vale 7, pois esse elemento está localizado na segunda linha e quarta coluna.
Em uma matriz, a distribuição dos seus elementos é importante. Assim, para que duas matrizes sejam iguais, elas devem possuir a mesma dimensão e os mesmos elementos nas mesmas posições. Por exemplo, sejam as matrizes
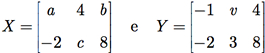
Para que X = Y, temos que ter obrigatoriamente a = -1, b = 4, c = 3 e v = 4.
Em muitos problemas práticos, surge um tipo de matriz chamada de matriz quadrada, na qual o número de linhas e o número de colunas são iguais. Se A é uma matriz quadrada n X n, então os elementos a11, a22, a33, ..., ann formam a diagonal principal da matriz.
Outro tipo especial de matriz surge quando imaginamos dobrar uma matriz quadrada ao meio ao longo da diagonal principal, e os elementos que se sobrepõem são iguais. Nesse caso, temos uma matriz simétrica, na qual aij = aji. Por exemplo, considere a matriz
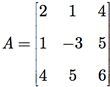
A matriz A é quadrada com dimensão 3 X 3 e também é simétrica. A parte triangular superior (a parte acima da diagonal principal) é uma reflexão da parte triangular inferior. Ainda observe que a12 = a21 = 1, a13 = a31 = 4 e a23 = a32 = 5.