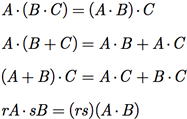G.2 Operações Matriciais
Multiplicação por um Escalar
Essa operação multiplica cada elemento de uma matriz por um único valor fixo, chamado escalar. O resultado é uma matriz com a mesma dimensão que a matriz original.
Exemplo G.1: Multiplique a matriz A pelo escalar r = 2.
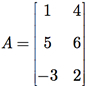
Nesse caso, queremos determinar a matriz B = r × A. Assim, temos que
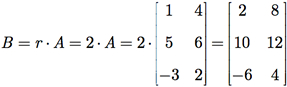
Soma de Matrizes
A soma de duas matrizes A e B apenas está definida quando as matrizes possuem a mesma dimensão. Nesse caso, somamos os elementos correspondentes das matrizes. Matematicamente, se A e B são matrizes m X n, então C = A + B é uma matriz também m X n com elementos
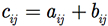
Exemplo G.2: Some as matrizes A e B a seguir.

Temos, então, que
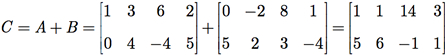
Observações Importantes
a) A subtração de matrizes é definida por A - B = A + (-1) × B.
b) Em uma matriz nula, todos os seus elementos são iguais a zero. Se somarmos uma matriz nula m X n a qualquer outra matriz A, também m X n, o resultado é a própria matriz A. Isso pode ser simbolizado por 0 + A = A.
c) Se A e B são matrizes m X n e se r e s são escalares, as seguintes equações matriciais são verdadeiras:
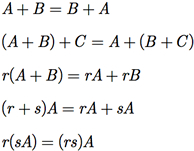
Multiplicação de Matrizes
A definição do produto de matrizes é baseada na utilização de matrizes em matemática para representar certas funções, conhecidas como transformações lineares, que levam pontos do plano real em pontos do plano real.
Assim, para efetuarmos o produto entre duas matrizes A e B, o número de colunas de A deve ser igual ao número de linhas de B. Então, podemos calcular A × B se A é uma matriz m X p e B é uma matriz p X n. O resultado será uma matriz com dimensão m X n. O elemento da matriz A × B na linha i, coluna j, é obtido multiplicando-se os elementos da linha i da matriz A pelos elementos correspondentes na coluna j da matriz B e somando-se todos os resultados. Matematicamente, temos que C = A × B com
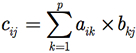
Exemplo G.3: Determine a matriz C = A × B.
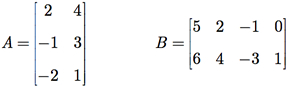
Inicialmente, observe que a matriz A é 3 X 2 e que a matriz B é 2 X 4, ou seja, o número de colunas de A é igual ao número de linhas de B. Portanto, podemos realizar o produto A × B, cujo resultado será uma matriz 3 X 4.
Para determinarmos o elemento c11 da matriz C, multiplicamos a linha 1 de A pela coluna 1 de B, somando os resultados, isto é,
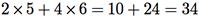
A Figura G.1 ilustra o procedimento descrito.

O elemento c12 é obtido multiplicando a linha 1 de A pela coluna 2 de B, somando os resultados, isto é,
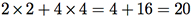
A Figura G.2 ilustra o procedimento.

O produto completo é
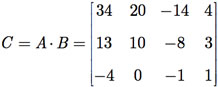
Exemplo G.4: Dadas as matrizes A e B, calcule C = A × B e D = B × A.
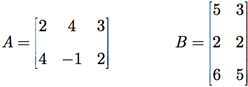
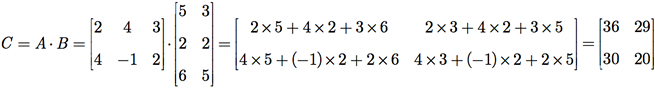
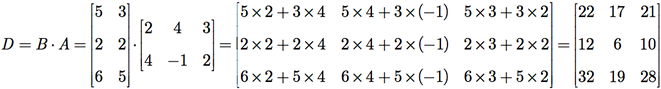
Exemplo G.5: Repita o Exemplo G.4 para as matrizes

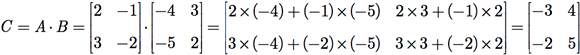
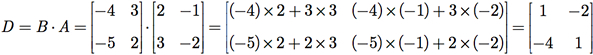
Dos resultados dos Exemplos G.4 e G.5, concluímos que, mesmo as matrizes A e B tendo dimensões que permitam realizar os produtos A × B e B × A, esses produtos não são necessariamente iguais.
Relações Importantes
Se A, B e C são matrizes de dimensões apropriadas e se r e s são escalares, as equações matriciais a seguir são verdadeiras: