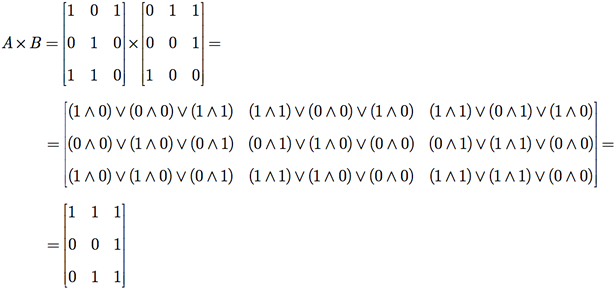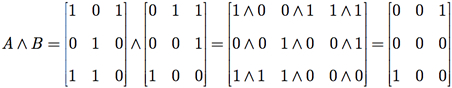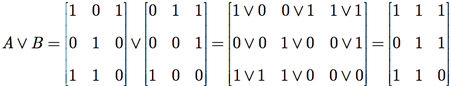G.6 Matrizes Booleanas
As matrizes booleanas (em homenagem a George Boole, um matemático inglês do século XIX, criador da lógica e da álgebra booleana) são um tipo especial de matrizes nas quais os seus elementos valem 0 ou 1. Por exemplo, a matriz A é uma matriz booleana
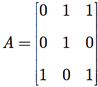
Nesse contexto, os valores 0 e 1 são interpretados como valores lógicos ou valores booleanos. Para os valores booleanos, podem ser definidas as seguintes operações:
- multiplicação booleana: x ∧ y = min(x, y)
- soma booleana: x ∨ y = max(x, y)
onde min e max significam, respectivamente, valor mínimo e valor máximo entre x e y.
De acordo com essas definições, podemos montar tabelas para a multiplicação e soma booleanas, conforme mostrado nas Figuras G.3 e G.4.
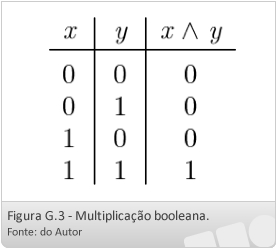
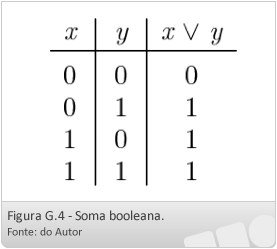
Baseados na multiplicação booleana e na soma booleana entre valores, podemos definir a operação de multiplicação booleana entre duas matrizes A e B (matrizes booleanas com dimensões apropriadas), denotada por A × B. Os elementos da matriz booleana C = A × B são dados por
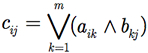
Nós podemos também definir dois análogos da soma para as matrizes booleanas (matrizes com mesmas dimensões): A ∧ B, onde os elementos correspondentes são combinados usando-se a multiplicação booleana; e A ∨ B, onde os elementos correspondentes são combinados usando-se a soma booleana.
Exemplo G.8: Dadas as matrizes booleanas
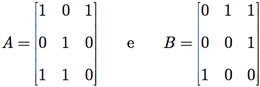
calcule A × B, A ∧B e A ∨B.