H.1 Definições e Exemplos
Vamos começar analisando uma forma bem conhecida de aritmética, a soma de inteiros. Existe um conjunto Z de objetos (o conjunto dos números inteiros) e uma operação binária nesses objetos (a soma). Não podemos esquecer a Unidade D do nosso Curso. Uma operação binária em um conjunto tem que ser bem definida (dar uma única resposta sempre que for aplicada a dois elementos do conjunto) e o conjunto tem que ser fechado em relação à operação (a resposta tem que ser um elemento do conjunto). A notação [ Z , +] denota o conjunto com a operação binária.
Em [Z, +], uma equação do tipo
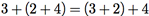
é válida. Em cada lado da igualdade, os inteiros permanecem na mesma ordem, mas o agrupamento desses inteiros, que indica a ordem em que são efetuadas as somas, se altera. A alteração dessa ordem, porém não influi no resultado final, que continua o mesmo.
Um outro tipo de equação que é válida em [ Z , +] é
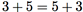
Nesse caso, a mudança da ordem em que os inteiros são somados não altera o resultado final.
Equações do tipo
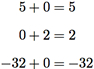
também são válidas. Somar zero a qualquer inteiro não altera o valor desse inteiro.
Por fim, equações do tipo
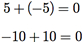
também são válidas, pois somar o negativo de um inteiro a esse inteiro resulta em zero.
Essas equações representam quatro propriedades bastante frequentes com operações binárias em conjuntos.
Definições: Propriedades de Operações Binárias: Seja S um conjunto e seja Δ uma operação binária em S.
a) A operação Δ é associativa se
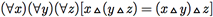
A associatividade nos permite escrever x Δ y Δ z sem parênteses, pois o agrupamento não é relevante.
b)A operação Δ é comutativa se
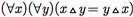
c)[S, Δ] tem um elemento identidade se
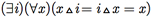
d) Se [S, Δ] tem um elemento identidade i, então cada elemento em S tem um inverso em relação a Ω se
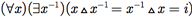
Definições: Grupo e Grupo comutativo: [S, Δ] é um grupo se S é um conjunto não vazio e Ω é uma operação binária em S tal que:
- V é associativa;
- existe um elemento identidade em S;
- cada elemento em S tem um inverso em relação a V.
Um grupo em que a operação Δ é comutativa é chamado de grupo comutativo.
Do apresentado anteriormente, verificamos que [Z, +] é um grupo comutativo com elemento identidade 0.
Exemplo H.1: Seja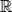 
+ o conjunto dos números reais positivos e × a operação de multiplicação entre dois números reais, que é uma operação binária em 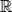+. Então, [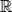+, ×] é um grupo comutativo. A multiplicação é associativa e comutativa. O número real positivo 1 funciona como uma identidade, pois
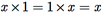
para todo número real positivo x. Todo número real positivo x tem um inverso em relação à multiplicação, que é o número 1/x, pois
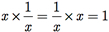
Exemplo H.2: Considere M2(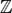
) o conjunto de todas as matrizes 2 × 2 com elementos inteiros e seja + a soma de matrizes. Então + é uma operação binária em M2(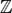). Portanto, [M2(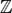), +] é um grupo comutativo, pois os inteiros formam um grupo comutativo, de modo que cada elemento da matriz se comporta apropriadamente.
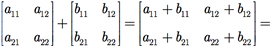
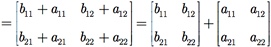
A matriz
é uma identidade; e a matriz
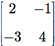
é a inversa em relação à operação de soma de matrizes da matriz
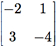
Exemplo H.3: Considere [M2(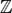), •], onde × é a operação de produto matricial. Essa operação é fechada em M2(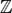). Sabemos também, da Unidade G, que a multiplicação de matrizes é associativa. Além disso, a matriz
é um elemento identidade para a operação •, pois
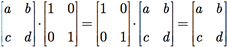
Porém a operação do produto matricial não é comutativa e não apresenta elemento inverso pertencente ao conjunto M2(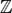). Portanto, [M2(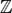), •] não é um grupo.
Exemplo H.4: Uma expressão da forma
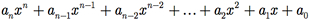
onde ai ∈ 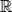, i = 0, 1, 2, ..., n e n ∈ 
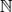é um polinômio em x com coeficientes reais (ou um polinômio em x sobre 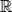). Para cada i, ai é o coeficiente de xi. Se i é o maior inteiro para o qual ai ≠ 0 e se i é maior do que 0, então o polinômio tem grau i; se não existe esse i, o polinômio tem grau zero. O conjunto de todos os polinômios em 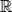sobre ¡ é denotado por 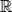[x].
Vamos definir a operação binária + em 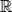[x] como sendo a operação usual de soma de polinômios. Se f(x) e g(x) são polinômio em 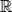[x], então as somas f(x) + g(x) e g(x) + f(x) são iguais, pois os coeficientes são números reais e podemos usar as propriedades dos números reais para a soma.
Temos também que, se f(x), g(x) e h(x) são polinômios em 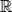[x], (f(x) + g(x)) + h(x) é igual a f(x) + (g(x) + h(x)). O polinômio constante 0 é a identidade, pois 0 + f(x) = f(x), para todo f(x) ∈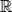[x]. E, além disso, o polinômio -f(x) é a inversa em relação à operação de soma de polinômios, pois -f(x) + f(x) = f(x) + (-f(x)) = 0.
Portanto, [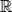[x], +] é um grupo comutativo.
Exemplo H.5: Em relação ao grupo [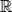[x], +] do Exemplo H.4, qual é o elemento inverso do polinômio 3x3 - 2x2 + 5x - 7?
É o polinômio -3x3 + 2x2 - 5x + 7.
Uma forma visual de analisar se um conjunto e uma operação binária definida nesse conjunto é um grupo é através de uma tabela. Considere [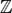, +]. A Tabela H.1 mostra as relações entre os elementos do conjunto 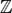em relação à operação +.
Tabela H.1 Tabela para o grupo [, +].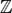
Para verificar a comutatividade, basta verificar se existe simetria em relação à diagonal principal da tabela.
Para determinar se existe o elemento identidade, basta verificar se, no interior da tabela, existe uma coluna que seja igual à coluna externa da tabela. Se existir, o elemento na coluna externa é a identidade. Ou, de forma alternativa, verificar se existe uma linha interna da tabela que seja igual à linha externa da tabela. Se existir, o elemento na linha externa é a identidade.
Para localizar se existe o elemento inverso, procure na linha correspondente até encontrar a coluna onde aparece a identidade; depois, verifique ainda se a mudança de ordem ainda resulta na identidade.
A propriedade associativa (ou a falta dela), no entanto, não é fácil de ser verificada através da tabela.
Exemplo H.6: Considere um conjunto A e seja SA o conjunto de todas as funções permutação f:A → A.
A composição de funções o preserva as permutações e é associativa, a função identidade iA é uma permutação e, qualquer que seja f ∈ SA, a função inversa f-1 existe e é uma permutação. Além disso,
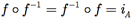
Portanto, podemos concluir que [SA, o] é um grupo. Esse grupo é chamado de grupo de permutações de A.
Exemplo H.7: Se o conjunto A = {1, 2, 3, ..., n} para algum inteiro positivo n, então SA é chamado de grupo simétrico de grau n e denotado por Sn.
Por exemplo, S3 é o conjunto de todas as permutações de {1, 2, 3}. Existem seis permutações, que usando a notação de ciclos da Seção E.6.1, são: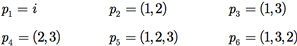
Recordemos que a notação de ciclo (1, 2), por exemplo, significa que 1 vai em 2, 2 vai em 1 e os elementos que não aparecem permanecem fixos. A composição (1, 2) o (1, 3) é executada da direita para a esquerda, de modo que
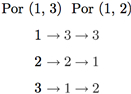
resultando em (1, 3, 2). Logo, p2 o p3 = (1, 2) o (1, 3) = (1, 3, 2) = p6. Seguindo esse procedimento, vamos construir a tabela para o grupo [S3, o], a qual está mostrada na Tabela H.2.
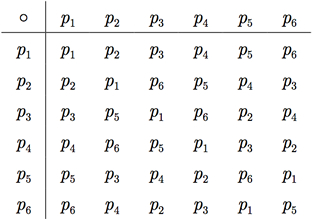
Tabela H.2 - Tabela para o grupo [S3,o]
Observando a Tabela H.2, notamos que não há simetria em relação à diagonal principal.
Portanto, [S3, o] não é um grupo comutativo.