H.2 Resultados Básicos Sobre Grupos
Teorema sobre a Unicidade da Identidade em um Grupo: Em qualquer grupo [F,Δ], o elemento identidade i é único.
Teorema sobre a Unicidade de Inversos em um Grupo: Para cada elemento y em um grupo [F,Ω], y-1 é único.
Teorema sobre o Inverso de um Produto: Se x e y pertencem ao grupo [F, V], então (x V y)-1 = y-1 V x-1.
Definição: Regras de Cancelamento: Um conjunto S munido de uma operação binária Δ satisfaz a regra de cancelamento à direita se, quaisquer que sejam x, y, z ∈ S, x Δ z = y Δ z implica em que x = y. Ele satisfaz a regra de cancelamento à esquerda se, quaisquer que sejam x, y, z ∈ S, z Δ x = z Δ y implica em que x = y.
Teorema sobre Cancelamento em um Grupo: Qualquer que seja o grupo [F, Δ], ele satisfaz as regras de cancelamento à direita e à esquerda.
Se [F, Δ] é um grupo, onde F é finito e possui n elementos, então n é a ordem do grupo e é denotada por |F|. Se F é um conjunto infinito, então o grupo tem ordem infinita.
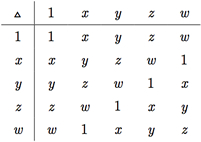
Exemplo H.8: Seja Δ uma operação binária associativa no conjunto {1, x, y, z, w}. Complete a tabela a seguir de modo a definir um grupo com identidade 1.

A solução é