H.3 Subgrupos
Definição: Subgrupo: Sejam [F, Δ] um grupo e A Í F. Então, [A, Δ] é um subgrupo de [F, Δ] se [A, Δ] for um grupo.
Teorema sobre Subgrupos: Sejam [F, Δ] um grupo com identidade i e A ⊆ F. Então, [A, Δ] é um subgrupo de [F, Δ] se satisfaz as seguintes condições:
- A é fechado em relação a Δ;
- i ∈ A;
- todo x ∈ A tem um inverso em A.
Observação: as propriedades da operação binária ser bem definida e ser associativa, de fato, não precisam ser verificadas pois, como A ⊆ F, A herda essas propriedades de F (F é um grupo).
Exemplo H.9: Sejam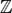 
o conjunto dos números inteiros, A o conjunto dos números inteiros pares e + a operação de adição. Assim, A é fechado em relação à adição, contém 0 (o elemento identidade) e o inverso de qualquer inteiro par (seu negativo) é um inteiro também par. Logo [A, +] é um subgrupo do grupo [, +].
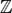Exemplo H.10: Considere o Exemplo H.9, onde A agora é o conjunto dos números inteiros ímpares. Nesse caso, [A, +] não é um grupo por várias razões. [A, +] não é fechado em relação à adição, visto que a soma de dois inteiros ímpares é um inteiro par. Outro motivo é que o subgrupo deve ter uma identidade para a adição; 0 é o único inteiro que serve e 0 não é ímpar.
Exemplo H.11: [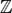, +] é um subgrupo do grupo [
, +].
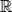Teorema de Lagrange: A ordem de um subgrupo de um grupo finito divide a ordem do grupo.